虽然 dwl 老师确实很好，但是我感觉初概这课有点儿稀碎（个人意见，个人意见）。

先前把统辅当做很有趣的数学分支，被转数环的学长泼了冷水说“统计中心的风格可能会不大适应”，另一位学长也说“统辅不是你期待的样子”，目前看中心开课的意思也好像有点当工科的辅助来学。我到底多大程度上能接受严谨的数学推导？又能走多远？统辅还是数辅~~还是我全都要~~，这是一个问题。

初概这玩意儿前八周上完，约等于梦回高中月考，我定义呢我证明呢啊怎么直接拿来用了？在考虑下学期去数学系重新上概（1），甚至考虑跟实复分析，但是数分的空缺真的没问题吗。当然，没有退初概还是为了跟上统辅的进度，毕竟后八周还有统计推断，我也没完全放弃统辅，目前或许是我目光短浅了。

这门课和教材也没什么映射关系（而且看老师的意思是也没有教材，草），直接按照 Lecture n 的顺序写吧。本来想放进茴香豆篇，但概率论这边举例比较多，放在一起又很冗长，还是算了。

Lecture 1

概率模型：概率模型由样本空间和概率构成。每一个概率模型都关联着一个试验。
- 样本空间是一个集合，概率模型对应的试验产生的所有可能结果形成样本空间，记作 $\Omega$。比如说，概率模型为抛硬币，样本空间即为 $\lbrace head,tail \rbrace$。样本空间可以是离散的，也可以是连续的。
- 事件 $A$ 是样本空间的子集，也就是某些试验结果的集合。概率 $P(A)$ 分配到事件 $A$ 上。
概率公理：非负性，归一化，可加性。
概率的性质：两个技巧，归纳法和取补集。

Lecture 2

事件域（或称为 $\sigma-$域，$\sigma-$代数）：对于样本空间 $\Omega$，$F$ 表示 $\Omega$ 的某些子集构成的集合，如果 $F$ 满足以下三个条件：
- $\Omega \in F$ ；
- 对于任意的 $A\in F$，有 $A^c \in F$；
- 如果 $A_n \in F$，$n=1,2,...$，则 $\cup_{n=1}^\infty A_n \in F$。
那么称 $F$ 为 $\Omega$ 上的事件域，称 $F$ 中的元素为事件，称 $(\Omega,F)$ 为可测空间。

从而，有且只有 $F$ 中的每个事件都能分配概率，这就圈定了我们所关心的事件的范围。

事件域的一些性质如下：
- 两个事件域的并集不一定是事件域，但交集一定是。（Trivial）
- 事件域对集合的任何计算都是封闭的，包括事件列的极限运算。
概率，也称为概率测度：设 $(\Omega,F)$ 为可测空间，$P$ 是定义在 $F$ 上的函数，如果 $P$ 满足以下三个条件：
- 非负性，完全性（Trivial）
- 可列可加性（$\sigma-additivity$）：对于 $F$ 中互不相交的事件 $A_1,A_2,...$ ，有 $P(\cup _{n=1} ^\infty A_n) = \Sigma _{n=1} ^\infty P(A_n)$。
那么称 $P$ 为 $F$ 上的概率测度，简称概率。
对于上述定义的样本空间，事件域和概率测度，我们称 $(\Omega,F,P)$ 为概率空间。

简单举个例子，在掷硬币的概率模型中，样本空间是 $\lbrace Head,Tail \rbrace$，事件域是 $\lbrace \lbrace Head,Tail \rbrace, \lbrace Head \rbrace, \lbrace Tail \rbrace, \emptyset \rbrace$，此时样本空间和事件域构成可测空间。事件域中的每一个元素都是事件，概率测度为 $P(\lbrace Head \rbrace) = p$, $P(\lbrace Tail \rbrace)=1-p$。（这是考虑了 $biased$ $coin$ 的情况）
概率测度的一些性质：
- 对于单调增序列，有 $\lim_{n \to \infty} A_n = \cup_{i=1} ^\infty A_i$， $P(\lim_{n \to \infty}A_n) = \lim_{x \to \infty}P(A_n)$。
- 单调减序列同理。
条件概率（定义略）的若干性质：
- 对互不相容的事件列 $B_i $，有 $P(\cup _{i=1}^\infty B_i|A) = \Sigma _{i=1} ^\infty P(B_i |A)$。
- 用 $P_A(·)=P(·|A)$ 表示在事件 $A$ 发生条件下的条件概率，这仍然是一个概率测度，$(\Omega,F,P_A)$ 仍然是一个概率空间。
  
  当然，此时我们可以把 $A$ 之外的结果排除掉，记作 $(A,A\cap F,P_A)$。
乘法公式：设 $(\Omega, F,P)$ 是概率空间，$A_i \in F$，$i = 1,2,...,n$，且 $P(A_1 \cap A_2 \cap ... \cap A_{n-1})>0$，于是有$P(\cap_{i=1}^n A_i) = P(A_1) \Pi_{i=2}^n P(A_i|A_1\cap A_2 \cap ... \cap A_{i-1})$。

举个例子：某人写了 $n$ 封信，将其装入 $n$ 个写有地址的信封，全部装错的概率 $q_0$ 为？恰有 $r$ 个信封装对的概率 $q_r$ 为？
- 在第一个问题下面，我们考虑记事件 $A_i$ 为第 $i$ 个信封装对的事件，利用容斥原理即可。
- 在第二个问题下面，其实问题主要在于怎么考虑是哪 $r$ 个信封放对了的问题。“指定的某 $r$ 个信封放对了”这一事件的概率等于“从 $n$ 个信封里无放回地取出 $r$ 个正好是前 $r$ 号”的概率。又因为从 $n$ 个信封里指定 $r$ 个有 $C_n ^r$ 种方式，于是这一部分的概率为 $\frac{1}{r!}$。
全概率公式：将 $\Omega$ 分割成事件 $A_1,A_2,...,A_n$ 的并，另有其中的事件 $B$，可以对每个 $i$ 得到 $P(B|A_i)$，于是 $P(B) = \Sigma_{i=1}^n P(A_i)P(B|Ai) = \Sigma_{i=1}^n P(B \cap A_i)$。

这个时候，我们称 $\lbrace A_i \rbrace$ 是 $\Omega$ 的一个分割。同时，式中的 $n$ 可以用 $\infty$ 代替。

举个例子：一个袋子里有 $n$ 个白球和 $m$ 个黑球，从中无放回地取出 $k$ 个球，求第 $k$ 次取得黑球的概率。
- 递归：第一次取黑球的概率影响第二次，第二次影响第三次...简单列个数列可以看出来取黑球的概率是定值，即为 $\frac{m}{m+n}$。
- 排队：把 $m+n$ 个球排成一列，算第 $k$ 个恰为黑球的概率即可。
$Bayes$ 准则：设 $(\Omega,F,P)$ 是概率空间，$B,A_i \in F$，$i=1,2,...,n$，$\lbrace A_i \rbrace$ 是 $\Omega$ 的一个分割。我们要用 $P(B|A_i)$ 算 $P(A_i|B)$，就可以使用 $Bayes$ 准则：$P(A_i|B)=\frac{P(A_i)P(B|A_i)}{\Sigma_{j=1}^n P(A_j)P(B|A_j)}$ 。

Lecture 3

（两两）独立性，条件独立性和一组事件的相互独立性
- 对于概率空间 $(\Omega,F,P)$，$A,B,C \in F$，独立性指的是 $P(A\cap B) = P(A)P(B)$，条件独立性指的是 $P(A\cap B|C)=P(A|C)P(B|C)$。
  
  那么这二者有什么关系呢？答案是没有关系（
  
  简单举个反例：抛掷两次均匀的硬币，令 $H_1=\lbrace$第一枚正面朝上$\rbrace$，$H_2=\lbrace$第二枚正面朝上$\rbrace$，$D=\lbrace$两枚硬币结果相反$\rbrace$。于是有 $P(H_1 \cap H_2) = P(H_1)P(H_2)$，但是 $P(H_1 \cap H_2 |D) = 0,P(H_1|D) = \frac{1}{2}，P(H_2|D) = \frac{1}{2}$。也就是说，独立性不能推出条件独立性。
- 一组事件的相互独立性涉及到概率空间 $(\Omega,F,P)$ 中的一组事件 $A_1,A_2,...,A_n$，如果对于任意非空子集 $S\subset \lbrace 1,2,...,n \rbrace$，都有$P(\cap_{i \in S} A_i)=\Pi_{i\in S} P(A_i)$，那么称这一组事件是相互独立的。
  
  根据 $S$ 的完备性可以知道，两两独立性也不能推出一组事件的相互独立性。
- TODO：记得复习一下赌徒破产模型。
随机变量何种情况下是良定义的？
- 设 $(\Omega,F)$ 为可测空间，如果 $\Omega$ 上的函数 $X(\omega)$ 满足：对 $\forall x \in R$，$\lbrace \omega | X(\omega) \leq x\rbrace \in F$，则称 $X(\omega)$ 为 $(\Omega,F)$ 上的随机变量。

Lecture 4

对于离散型随机变量 $X$，称 $P(X=x_k) = p_k$ 为 $X$ 的概率分布，称 $\lbrace p_k \rbrace$ 为概率分布列，简称为 $PMF$。当其规律不够明显时可以写成表格形式。
- 两点（$Bernoulli$）分布：掷硬币或正或反，$P(X=0)=p,P(X=1)=1-p$。
- 二项（$Binomial$）分布：试验成功的概率为 $p$，重复 $n$ 次试验成功 $k$ 次的概率，$P(X=k) = C_n ^k p^k (1-p)^{n-k}$。它是二项式展开的其中一项，故名二项分布。
  
  二项分布的最大可能值（即中心项）的推断：考虑二项式展开。
- ......这里空间不够大，别的写不下了（其实是不需要记忆离散型分布的名字，会讲故事就行。
- 泊松（$Poission$）分布：$P(X=k)=\frac{\lambda ^k}{k!} e^{-\lambda}$。一般来说，记随机变量 $Y\sim P(\lambda)$ 表示 $Y$ 服从参数为 $\lambda$ 的泊松分布。
  
  放射粒子模型揭示了二项分布可以用泊松分布近似的事实。
  
  TODO：复习粒子模型，做书上习题 $2.2$。
对于连续型随机变量的定义如下：设随机变量 $X$，如果存在非负函数 $f(x)$ 满足对任意的 $a<b$，$P(a<X\leq b)=\int _a ^b f(x) dx$，则称 $X$ 为连续型随机变量。称 $f(x)$ 为 $X$ 的概率密度函数，简称概率密度或者密度（$PDF$）。

这并不意味着 $X(\omega)$ 是连续函数，因为样本空间可能没有任何的拓扑结构，谈不上连续性。
- 均匀（$Uniform$）分布：$f(x) = \frac{1}{b-a},x \in (a,b)$，此时记 $X \sim U(a,b)$。
- 指数（$Exponential$）分布：$f(x) = \lambda e^{-\lambda x},x\geq 0$，此时记 $X\sim \epsilon(\lambda)$。
  
  如果 $X$ 是连续型非负随机变量，则 $X$ 服从指数分布的充要条件是 $X$ 没有记忆性，也就是说 $P(X>s+t|X>s) = P(X>t)$。（可以由条件概率公式证出，Trivial.）
  
  $X$ 的失效率就是单位长度时间内失效的概率，可推知即为 $\lambda$。也称其为尺度参数（rate parameter）。
  
  TODO：再推一遍 $X\sim \epsilon(\lambda)$ 时，$Y=\lambda X$，则 $Y\sim \epsilon (1)$。
- 正态分布（$Normal$ $Distribution$）：$f(x)=\frac{1}{\sigma \sqrt{2 \pi}} exp(-\frac{(x-\mu)^2}{2\sigma ^2}),x \in R$，此时记 $X\sim N(\mu ,\sigma^2)$。
  
  正态分布的函数图像关于 $x=\mu$ 对称，在此处取最大值 $f(\mu) = (\sigma \sqrt{2\pi})^{-1}$。关于 $x=\mu \pm \sigma$ 处有拐点。

Lecture 5

概率分布函数（$CDF$）：对随机变量 $X$，称 $x$ 的函数 $F(x) = P(X\leq x),x \in R$ 为 $X$ 的概率分布函数，也称为累积分布函数，分布函数。
- 对一个 $PMF$ 书写 $CDF$，它一般是一个分段函数。
- 对一个 $PDF$ 书写 $CDF$，记随机变量 $X$ 的概率密度为 $f(x)$，则其分布函数为 $F(x) = \int_{-\infty}^x f(t) dt,x \in R$。对于一个已知的 $F(x)$，只能确定连续点 $x$ 处的概率密度为 $f(x) = F'(x)$，显然在不连续点处是无法确定的。
  - 注：连续型随机变量的概率密度不必为连续函数，允许可列个单点断开。那它为什么叫连续型呢？这与 $F(x)$ 的形式有关。同时离散型这一形容也与 $F(x)$ 有关。
- 举个例子：标准正态分布的概率密度为 $\phi(x)=\frac{1}{\sqrt{2 \pi}} exp(-\frac{x^2}{2}),x \in R$。其分布函数记为 $\Phi(x)$，其值需要查表，当然也可以丢进 MATLAB 算，但是不要求（
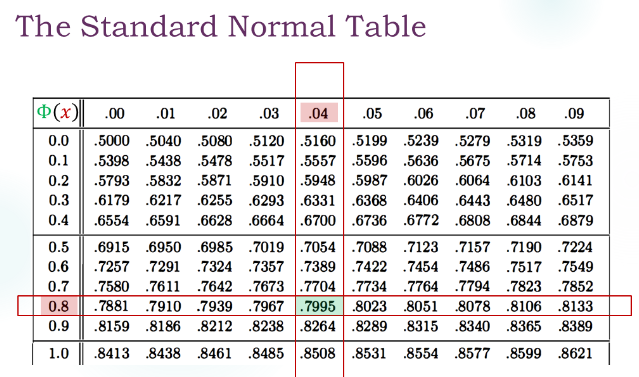
- 再举个例子：正态分布函数的概率密度计算中，可以对 $\frac{x-\mu}{\sigma}$ 进行换元，从而变为标准正态分布的情况。
- 再再举个例子：指数分布的分布函数要注意分段，考虑 $x<0$ 的情况。
  
  TODO：去看一下几何随机变量和指数随机变量的分布函数的逼近，这是利用 $CDF$ 寻找 $PMF,PDF$ 之间关系的例子。
- 分布函数对一切随机变量都适用，这是它相对 $PMF,PDF$ 的优势。
对于一个随机变量 $X$ 的函数 $g(X)$，怎么去寻找 $g(X)$ 的概率分布？（这一部分其实是做题方法）
- 最简单的情形：$X$ 是离散型随机变量，对每一个 $X$ 的取值 $x$，确定 $Y=g(x)$ 时的概率分布列即可。有需要的话还可以化成 $CDF$。
- 曲线救国：考察 $Y=g(X)$ 的分布，若 $g(x)$ 是连续函数，那么可以先得到 $Y$ 的 $CDF$ 为 $F_Y(y)=P(Y\leq y)$，再求导得到 $f_Y(y)=F_Y'(y)$。
- 特殊情况 1：线性的 $g(X)$ 可以直接从 $f_X(x)$ 得到 $f_Y(y)$ 而无需计算 $CDF$。
  
  形如 $Y=aX+b$ ，有 $f_Y(y)=\frac{1}{|a|} f_X(\frac{y-b}{a})$。（其实还是用 $CDF$ 证明的）
- 特殊情况 2：对于严格单调的 $g(x)$，考虑 $Y=g(X)$。记 $h(y)$ 是 $g(x)$ 的逆映射，于是 $f_Y(y)=f_X(h(y))|h'(y)|$，这可以通过考虑事件 $\lbrace x<X<x+\delta \rbrace$ 来证明。
- 特殊情况 3：像正态分布这样的特殊分布，遇到的时候建议先考虑能不能在 $\Phi(x)$ 的尺度先行利用对称性化简。

Lecture 6

$n$ 维随机向量：如果 $X_1,X_2,...,X_n$ 都是概率空间 $(\Omega,F,P)$ 上的随机变量，那么称 $X=(X_1,X_2,...,X_n)$ 为概率空间 $(\Omega,F,P)$ 上的 $n$ 维随机向量。

那么怎么从随机变量上迁移来诸多的概念呢？
- 联合概率分布函数：设 $X=(X_1,X_2,...,X_n)$ 为随机向量，称 $R^n$ 上的 $n$ 元函数 $F(x_1,x_2,...,x_n)=P(X_1<x_1,...,X_n<x_n)$ 为 $X=(X_1,X_2,...,X_n)$ 的联合概率分布函数，简称为联合分布或者分布函数。
- 有关离散型随机向量：如果 $X_1,X_2,...,X_n$ 都是离散型随机变量，则称 $X=(X_1,X_2,...,X_n)$ 为离散型随机向量。如果所有 $X_i$ 的不同取值为 $x(j_1,j_2,...,j_n)=(x_1(j_1),x_2(j_2),...,x_n(j_n))$，则称 $p_{j_1 j_2 ... j_n}=P(X=x(j_1,j_2,...,j_n))$ 是 $X$ 的联合分布列。
  - 举个例子：设 $F(x,y)$ 是 $(X,Y)$ 的联合分布，则 $X,Y$ 有概率分布：
    
    $F_X(x) = P(X \leq x,Y \leq \infty) = F(x,\infty)$，
    
    $F_Y(y) = P(X \leq \infty,Y \leq y) = F(\infty ,y)$。
    
    于是，对于矩形 $D=\lbrace a<X \leq b,c < Y \leq d \rbrace$，有 $P((X,Y)\in D) = F(b,d)-F(b,c)-F(a,d)+F(a,c)$。
- 有关连续型随机向量：简单来说，考虑二维的情形，如果 $(X,Y)$ 有联合密度 $f(x,y)$，则 $X$ 和 $Y$ 分别有概率密度 $f_X(x)=\int_{-\infty} ^{\infty} f(x,y)dy$，$f_Y(y)=\int_{-\infty}^{\infty} f(x,y)dx$。
  
  延拓到 $n$ 维的情况，被积函数 $f_k(x_1,x_2,...,x_k)=\int_{R^{n-k}} f(x_1,x_2,...,x_k) dx_{k+1}...dx_n$ 是为 $(X_1,...,X_n)$ 的联合密度，称之为边缘密度（Marginal PDF）。
- 连续型随机向量的独立性：对每个 $i(1\leq i \leq n)$，随机变量 $X_i$ 有概率密度 $f_i(x_i)$，则 $X_1,X_2,...,X_n$ 相互独立的充分必要条件为随机向量 $X=(X_1,X_2,...,X_n)$ 有联合密度 $f_1(x_1)f_2(x_2)...f_n(x_n),(x_1,x_2,...,x_n)\in R^n$。
- 经典连续型随机向量例：二元正态分布
  
  设 $\mu_1,\mu_2$ 为常数，$\sigma_1,\sigma_2$ 为正常数，$\rho \in (-1,1)$ 中的常数。如果随机向量 $(X,Y)$ 有概率密度
  
  $f(x,y)=\frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}}exp(-\frac{1} {2(1-\rho^2)} [\frac{(x-\mu_1)^2}{\sigma_1 ^2} + \frac{(y-\mu_2)^2}{\sigma_2 ^2} - \frac{2\rho (x-\mu_1)(y-\mu_2)}{\sigma_1 \sigma_2}])$，
  
  那么称 $(X,Y)$ 服从二元正态分布，记为 $(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2, \sigma_2^2, \rho)$。
  - 一些性质：$X,Y$ 独立的充要条件是 $\rho=0$。（Trivial）
- 联合分布（Joint CDF）与联合密度（Joint PDF）：已知联合密度 $f(x,y)$，于是有联合分布 $F(x,y) = \int _{-\infty} ^x \int _{-\infty} ^y f(u,v)dudv$。
  
  当 $f(x,y)$ 连续时，有 $f(x,y) = \frac{\partial^2 F(x,y)}{\partial x \partial y}$。更一般地，如果该混合偏导数不存在，那么 $f(x,y)=0$。
- 连续型条件概率分布：设随机向量 $(X,Y)$ 有联合密度 $f(x,y)$，$Y$ 有边缘密度 $f_Y(y)$。若在确定的 $y_0$ 处 $f_Y(y_0)>0$，则称 $P(X \leq x | Y=y_0) = \frac{\int_{-\infty} ^x f(s,y_0) ds}{f_Y(y_0)}$ 为给定条件 $Y=y_0$ 下，$X$ 的条件分布函数（conditional CDF），记为 $F_{X|Y}(x|y_0)$。
  
  于是条件分布密度为 $f_{X|Y}(x|y_0) = \frac{f(x,y_0)}{f_Y(y_0)}$。（conditional PDF）
  - 一些性质：
    
    $F_{X|Y}(x|y)=P(Xx|Y=y)={-} ^x f{X|Y}(s|y)ds, x R $。
    
    如果 $F_{X|Y}(x|y)$ 关于 $x$ 连续，且除去至少可列个点后有连续的导数，则在偏导数存在时，$f_{X|Y}(x|y_0)=\frac{\partial F_{X|Y}(x|y)}{\partial x}$，否则为 $0$。

期中插播提示

关于连续型概率分布之前的误解：连续型的随机变量不能随便取单点的概率，因为单点处的概率就是 $0$，这就是为什么要定义一个概率密度的原因。概率密度的大小可以是任意的，不一定要小于 $1$，只要它的积分能够表示某一段（区域）的概率即可，这个在联合分布中有比较多的体现。

总之，虽然 $F(x,y) = \int_{-\infty}^x \int_{-\infty}^y f(u,v)dudv$，但是 $f(u,v)$ 不等同于 $P(X=u,Y=v)$。同理，如果要算条件概率的话，可以用 $F_{X|Y}(x|y)=P(x_1\leq X\leq x_2|Y=y)=\int_{x_1}^{x_2} f_{X|Y} (s|y)ds$，也就是对 cond PDF 来积分求解。

（但是，出于记忆公式的方便考虑，我还是会把它当成单点处的概率来列写公式（
关于随机变量的独立性，定义如下：设 $X_1,X_2,...,X_n$ 是 $(\Omega,F)$ 上的随机变量，如果对任意的实数 $x_1,x_2,...,x_n$ 有 $P(X_1\leq x_1,X_2 \leq x_2,...,X_n \leq x_n)=P(X_1\leq x_1)...P(X_n\leq x_n)$ 成立，则称随机变量 $X_1,X_2,...,X_n$ 相互独立。

同时，设随机变量 $X_1,X_2,...,X_n$ 相互独立，$g_1(x),g_2(x),...,g_n(x)$ 是一元实可测函数，$\phi(x_1,x_2,...,x_k)$ 是 $k$ 元实可测函数，则：
- 随机变量 $g_1(X_1),...,g_n(X_n)$ 相互独立；
- 随机变量 $\phi(X_1,...,X_k),X_{k+1},...,X_n$ 相互独立。
这在样题的某个判断题中，以离散型随机变量的形式出现了，于是我自己证明了一下。实际上是一个更一般的结论。
单调事件列的概率极限问题：以单调增序列 $\lbrace A_i\rbrace$ 为例，有结论 $lim_{n\to \infty} A_n=\cup _{i=1}^{\infty} A_i$，于是极限概率为：

$P(\cup _{i=1}^{\infty} A_i) = P( lim _{n\to \infty} A_n) = lim _{n \to \infty} P(A_n)$。

对于一些不单调的事件序列，可以用交并补构造一个单调序列，使得可以使用上述规律。
事件列的上下极限的通俗说法：设 $\lbrace A_i \rbrace$ 是 $\Omega$ 中的一个事件列，定义上下极限为：

$lim_{n\to \infty} sup A _n = \cap _{n=1}^{\infty} \cup _{k=n}^{\infty} A_k =\lbrace \omega \in \Omega: \omega$ 属于无穷多个 $A_i\rbrace$。

$lim_{n\to \infty} inf A _n = \cup _{n=1}^{\infty} \cap _{k=n}^{\infty} A_k =\lbrace \omega \in \Omega: \omega$ 属于所有的 $A_i$ 除去有限个$\rbrace$。

当上下极限相等时称 $\lbrace A_i \rbrace$ 的极限存在。
条件概率中会忘记的常识：对互不相容的事件列 $\lbrace B_i \rbrace$，有 $P(\cup _{i=1}^{\infty} B_i | A) = \Sigma _{i=1}^{\infty} P(B_i | A)$。

一个 insight：求条件概率时我们可以把 $A$ 之外的结果排除掉，记作 $(A,A\cap F,P_A)$，这个事件域上完全可以有概率分布，因此不必为折棒太郎题惊讶。
注意一组事件“相互独立”所要求的完备性。
复习指南：
- 以上全部 TODO
- 去看一下习题课中《一个有助于理解独立性的题目》和 Polya 坛子问题第二问。
- Poisoner's Dilemma
- A family has two girls while at least one names Lilia
- 记一下几个重要分布，以及二元正态
- 过一遍离散型、连续型随机向量的独立性证明，二元正态分布的独立性证明。
- ~~折棒太郎~~折木棍问题的随机向量表述，Buffon 问题
最后是一个我比较个人向的整理，根据考试重点和过往习题。Click Here
记得多用归纳！

Lecture 7

又是全新的一门课辣（自我洗脑）

『姑妄言之姑妄听之』

初等概率论与挣扎