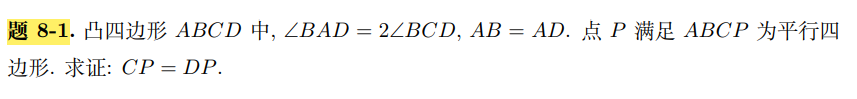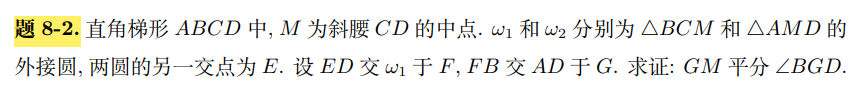2022 Sharygin Geometry Olympic 题解小记

今年是第三次写 Sharygin Geometry Olympic 题解，可能是最后一次。所以我又来水字数了

退役两年人员写几何题快裂开了，从来没觉得做题这么难过。但是蛮好玩的，什么叫思维体操啊（

只做了一点微小的贡献，谢谢大家。

显然，本人不善几何。尤其是自己的通讯地址变成华子之后水平骤降，每次都是替大家扫水题，然后排最后一个。其实这次论数量论质量都应该是排第四的，但是为了给新成员让路所以还是排最后了...啊就这样吧 XD，也不重要。还是看看远处的 SRT 吧家人们

在新星发文章的最高记录是二作，大概是 2020 Vietnam Mathmatics Olympic。成员们来来去去，最年轻的也马上高三了，或许是最后一次合作，起码我应该不会再参加了。

第一次在电脑上用 Geogebra，之前都是在手机上用，电脑上用 Sketchpad。Geogebra 上手莫名很快，手感也很熟悉，再一想发现快捷键和 AutoCAD 一模一样，这下职业病了。然后也是第一次尝试用 tikz 在 LaTeX 文档里插图，感觉还挺好用，赞美。

另外，谁能想到我五个几何题做了一天呢（思维体操，思维体操.jpg

8-1

非常水，我甚至能 15 分钟解决（

Sharygin2022.pdf（策划不给源代码，可恶（？

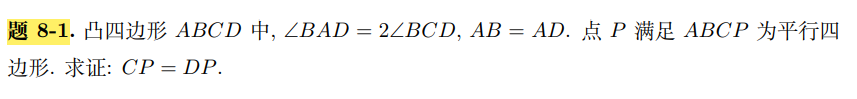
Sharygin-by-Chiyuru.tex

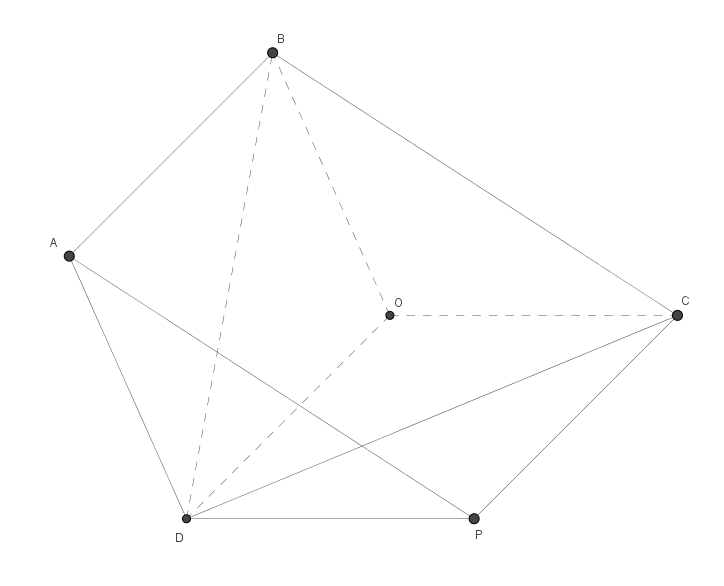
\textbf{8-1 证明:}取$\triangle BCD$的外心为$O$.于是有$OB=OD,AB=AD$,由于
	
$\angle DBO=90^\circ -\angle BCD=90^\circ -\frac{1}{2}\angle BAD=\angle ABD$,
	
可知四边形$ABOD$为菱形.故有$CP=AB=OD$,且
	
$\angle DCP=180^\circ -\angle ABC-\angle BCD=180^\circ -(\angle ABD+\angle BCD)-\angle DBC=90^\circ -\angle DBC=\angle ODC$
	
于是$OD,CP$互相平行且相等,则四边形$OCPD$为平行四边形,有$CP=OD=OC=DP$,得证.\qed
	
\textbf{评注:}题目中的二倍角条件几乎明示了作圆心，连出辅助线后即得解。

8-1.ggb（tikz 看起来丑丑的？

8-2

稍微有点痛，但是也还好，还是水题。

Sharygin2022.pdf

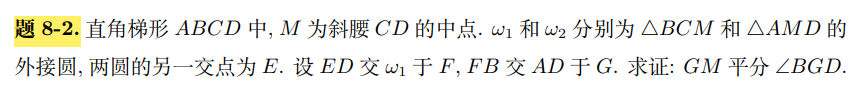
Sharygin-by-Chiyuru.tex

\textbf{8-2 证明:}取$\omega_1$与$AB$的交点为$E'$.
    
有$\angle CME'=\angle CBE'=\angle ME'A=90^\circ$.可知$M,E'A,D$四点共圆,$\omega_1$与$\omega_2$的交点$E$与$E'$重合,在$AB$上.
    
故$\angle CFD=\angle CBE=90^\circ$,$M$为斜边$CD$中点,即$MF=MD=CM$.
    
又注意到$\angle AGB=\angle CBF=\angle FMD$,即得$M,F,G,D$四点共圆,则$\angle BGM=\angle MDF=\angle MFD=\angle MGD$,得证.\qed
	
\textbf{评注:}作图准确的话可以很快得到$E$在线段$AB$上的结论，倒角即得解。

8-2.ggb

策划说他写了个脚本批量修改 tikz 的格式，我们只要交个 .ggb 就好了。所以我前两张图的线粗细都不一样，测试一下（

8-4

这个题太痛了，我想了有一个多小时，然后发现自己好傻。

Sharygin2022.pdf

Sharygin-by-Chiyuru.tex

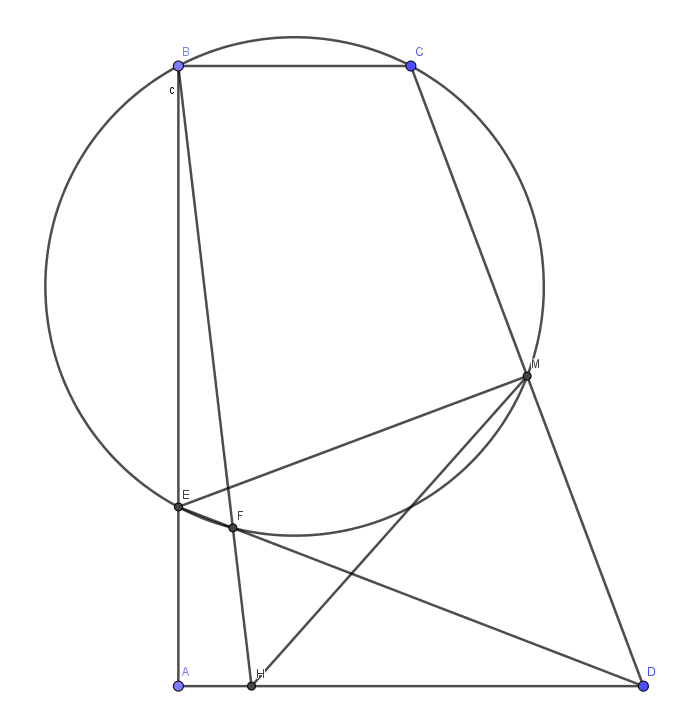
\textbf{8-4 证明:}取$\astrosun (OPN)$ 和$CD$的另一交点为$S$,$\astrosun (OPM)$和$AB$的另一交点为$T$.
联结$SC_1,SD_1,B_1T,A_1T,SP,PT,ON,OM$.
    
由$\angle SPO=\angle OND=\angle OMA=\angle OPT=90^\circ$,知$S,P,T$三点共线.
    
考虑到$\triangle PDC$和$\triangle PAB$为相似三角形,其顶点与中点连线$PN,PM$、对应边的中垂线$ON,OM$的夹角对应地相等.即$\angle OSP=\angle ONP=\angle OMP=\angle OTP$.也即$\astrosun (OPN)$ 和$\astrosun (OPM)$的半径相等.
    
由此可知$SP=PT,SD_1=B_1T,SC_1=A_1T,A_1B_1=C_1D_1$.故$\triangle SD_1C_1 \cong \triangle TB_1A_1$.
    
考虑到$\angle OC_1P=\angle OA_1P$,从而有$OC_1=OA_1$.同时$OC=OA$,得到$C_1C=A_1A$.同理也有$B_1B=D_1D$.
过$T$作$TF \bot CA$,过$S$作$SE \bot CA$.由$SP=PT$可知$TF=SE$,结合$C_1C=A_1A$ 可知$\triangle AA_1T$和$\triangle CC_1S$面积相等,同理$\triangle BB_1T$和$\triangle DD_1S$面积相等.
    
结合$\triangle SD_1C_1 \cong \triangle TB_1A_1$可知,四边形$AA_1B_1B$与$CC_1D_1D$面积相等,得证.\qed

\textbf{评注:}本题大量运用了对称性，需要一定的几何直觉。作图准确的话不难发现两圆半径相等，从而迎刃而解。

《迎 刃 而 解》

8-4.ggb

8-7

这个最痛。组合几何，尤其是答案都出乎意料的组合几何，太痛了（

Sharygin2022.pdf

Sharygin-by-Chiyuru.tex

\textbf{8-7 解:}否。证明如下：
	
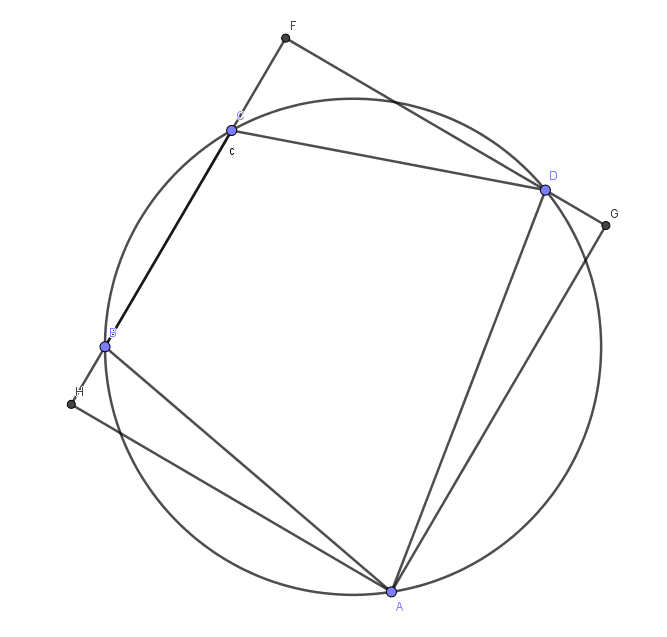
首先证明一个引理:对于共圆的四个点,它们一定位于某个正方形上.
	
不妨设共圆的四点为$A,B,C,D$,其中,四边形$ABCD$有至少两个角不是锐角，记为$\angle B,\angle C$.
两边延长$BC$,过$A,D$分别作$BC$的垂线$AH,DF$.不妨设$AH≥DF$,过$A$在$FD$的延长线上作垂线$AG$.从而四点$A,B,C,D$位于长方形$HFGA$上.若$HFGA$为正方形则引理已得证.
	
当$HF>FG$时,分别延长$HA,FG$至$A',G'$,使得$HA'G'F$为正方形,$A,B,C,D$在其上;当$HF<FG$时,同理分别延长$HF,GA$至$H',A'$即可.引理得证.
	
下面举出原命题的反例.取一个圆内接十边形的顶点,则它们不可能在同一个正方形上,这是因为一个正方形和圆最多有$8$个交点;同时,这$10$个点中的任意$4$个共圆,由引理知也即位于某一个正方形上.故原命题不一定成立,得证.
	
\textbf{评注:}本题的举例非常巧妙，笔者写作过程中的最大困难在于判断命题的对错，因此走了一段弯路。

8-7.ggb

9-1

这不比前面的都简单太多了？.jpg

Sharygin2022.pdf

Sharygin-by-Chiyuru.tex

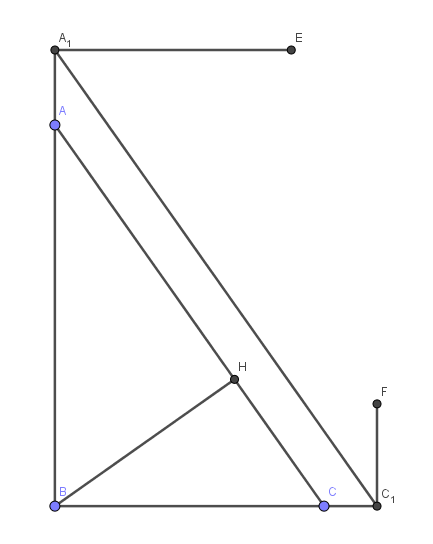
\textbf{9-1 证明:}
显然,$BC_1=\frac{1}{2} (BH+HC+CB),BA_1=\frac{1}{2} (BA+AH+BH)$.
	
于是$\frac{BC_1}{BA_1}=\frac{BH+HC+CB}{BA+AH+BH}=\frac{BC}{BA}$,从而$AC\parallel A_1C_1 $,得证.\qed

\textbf{评注:}非常基础的题目，熟知切点关于长度的结论即可。

9-1.ggb

后记与碎碎念

等到发表了（可能会拖到十月、十一月？）再来补个后记。其实就是丢个链接和文档，权当记录了。

看到行在清华公众号发的推文，才知道北京已经凉快些了，是初秋。上海还是每天都 40°C 左右，热得好难受。

这么说来，快要回去了。

后后记：Update 8-6

这个锅甩来甩去又回到了我手上，不会做，晚上把它翻译好了。

摸到了倒数第二作x。

Sharygin2022.pdf

Sharygin-8-6-by-Chiyuru.tex

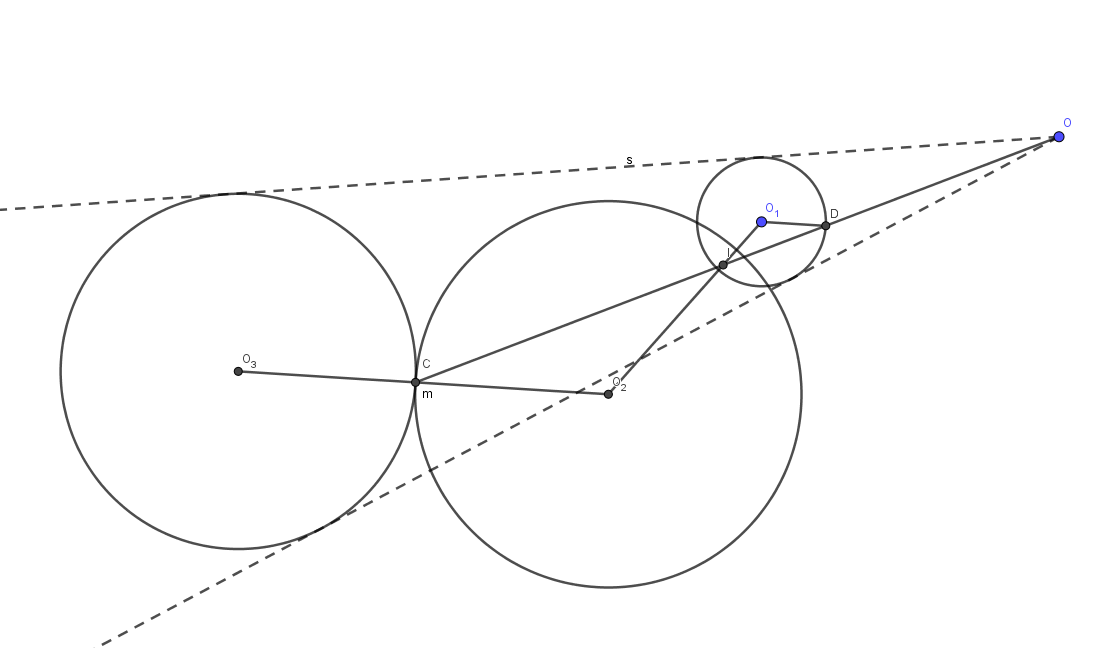
\textbf{8-6 解:}我们首先给出作图方式：
	
联结两圆$\omega_1、\omega_2$的圆心$O_1、O_2$,任取$\omega_1$上的点$T$并联结$O_2T$,作直线$O_1S\parallel O_2T$交$\omega_2$于$S$.取$ST$与$O_1O_2$的交点为$I$.
作射线$OI$分别交$\omega_1、\omega_2$于$D,C$,此即为$OC:OD$取最大值的情形.
	
证明:过$O$点以$OC:OD$为比例作$\omega_1$的外位似圆$\omega$,
易知$\omega$过点$C$.当$OC:OD$取最大值时,过$O$点以系数$k>OC:OD$为比例作$\omega_1$的外位似圆$\omega'$与$\omega_2$无交点.
	
因此$\omega$和$\omega_1$相切于$C$点.取$\omega$圆心为$O_3$,有$O_2,C,O_3$共线,且$O_2O_3\parallel O_1D$.故射线$ODC$与线段$O_1O_2$交于$\omega_1、\omega_2$的内位似中心，即为上述作出的$I$,得证.\qed
	
	
\textbf{评注:}尺规作图题中常见的利用位似性质的题目，非常精妙。

8-6.ggb