我觉得我写草稿纸上的笔记肯定过两天就不见了,存个档用来复习运筹期中,以及止增笑耳。
这什么破标题(
参考了《Applied Mathematical Programming》Chapter 9,10 和一份相应的 notes。
为什么要做 integer programming?一般来说 linear programming 也可以得到一个答案,把它 round 一下不就好了?但其实有一些很实际的理由导致 integer programming 是必须的,就像线性回归中 dummy variable 也是必须的一样(啥
一般来说把 integer programming 的 integer condition 移除后的 linear programming problem 称为其相应的 relaxed problem,integer programming 的 feasible set 一定是其 relax problem feasible set 的子集,其 optimal cost 也不会超过 relaxed problem 的 optimal cost。这很好理解,就是取了个限定更强的形式。
round 得到的结果未必还是最优的。比如:
\[\begin{aligned}\textbf{maximize} \quad & 8x_1+11x_2+ 6x_3 +4x_4 \\ \textbf{subject to} \quad & 5x_1+7x_2+4x_3+3x_4 \leq 14 \\ \quad &x_j \in \{0,1\}, \quad j=1,2,3,4 \end{aligned}\]
如果用 linear programming 会得到 optimal solution 是 \((1,1,0.5,0)^T\),round 一下得到 \((1,1,1,0)\) 并不在 feasible set 中。与此同时实际上的 optimal solution 是 \((0,1,1,1)^T\),哪怕反向 round 也得不到精确的结果。
但是每个通过 round 得到的结果都比真正的 integer programming 的 optimal cost 要小,某种程度上来说给出了一个估计。
integer programming 可以反映许多很难描述的条件。例如两个条件至多成立一个,用某个 integer variable 表示选择与否,等等。
哪怕真的可以用 round 的方法得到解,也不知道反向/正向 round 的结果是不是最好的,而在一些实际问题里哪怕只是相差 \(1\) 也会造成成本/效益的巨大差异。
另外 integer programming 的困难在于 optimal solution 不再一定在顶点处取到,而且 feasible set 是离散的点集,其数量远大于顶点数量,不太可能用枚举得到答案。
Standard Settings
Interger programming 的标准形式一般来说相对简单,但和 linear programming 稍有不同:
\[\begin{aligned} \textbf{maximize} \quad & c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & x_j \in \mathbb N \end{aligned}\]
其中要求 \(c \geq 0, A \geq 0, b \geq
0\)(指的是 \(A\) 的每个分量
\(a_{ij}\) 都要是非负的
而不是正定什么的要求)。
这样写相对粗糙。事实上,如果 \(A\) 只表示一个一维的 constraint 则称为 knapsack problem,否则是 multidimensional knapsack problem;如果所有的 \(x_j\) 均在 \(0,1\) 上取值则称为 pure integer programming,否则是 mixed linear programming。
对应的 pure integer programming 的标准形式是:
\[\begin{aligned} \textbf{maximize} \quad & c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & x_j \in \{0,1\} \end{aligned}\]
同样要求 \(c \geq 0, A \geq 0, b \geq 0\)。
Standardize to 0-1 Knapsack Problem
最明显的一些要求是 \(c\geq 0,A\geq 0\),至于 \(b\) 谋事在人成事在天(。
对于 1-dimension 来说一般来说如果有看到 \(c_i \geq 0, a_i \leq 0\) 的话直接把 \(x_i\) 取为 \(1\),因为这变相的扩容了 constraint 的上限;如果 \(c_i \leq 0 ,a_i \geq 0\) 则置为 \(0\),显然它的存在既会占用资源又减小上限。如果 \(c_i ,a_i \leq 0\) 同时成立就用 \(y_i = 1-x_i\) 代替原变量即可,从而得到标准形式。
Multidimension 咋办,他也没说啊(挠头(
感觉可能就不用动了,反正后面的求解里面都还是考虑 relaxed LP 问题,直接按照 LP 的 standardized form 来化简就可以。当然如果有一溜 \(\{a_{ij}\}_{i=1}^m \leq 0, c_i \geq 0\) 这种情况的话直接把 \(x_{i}\) 置 \(1\) 即可,少一个变量是一个。或者也可能是用 \(x_1\) 和 \(1-x_i\) 替换来保证所有的 \(c_i\) 为正。
Solutions to Integer Programming
Relaxed Linear Programming
比较符合直觉的一种方案就是把它和对应的 linear programming problem 结合起来看,它们之间的确存在一定的关系,甚至在某一些情况下可以得到对于 integer programming 的估计(未必是精确值)。
\[\begin{aligned} \textbf{maximize} \quad & c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & x_j \in \mathbb N \end{aligned} \quad \quad \quad \begin{aligned} \textbf{maximize} \quad & c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & x_j \geq 0 \end{aligned}\]
(暂且先不考虑 0-1 knapsack)
注意在实际计算中想要解出(比如用 simplex method)relaxed problem 还需要再做一步 standardize,此处略去。
此时有:
- 如果 LP 的 optimal solution 恰好是个 integer solution 那么也一定是 IP 的 optimal solution;
- LP 的 optimal cost 一定比 IP 的 optimal cost 更大;
- 如果 \(c\) 的所有分量也是整数,则将 LP 的 optimal solution 向下取整得到的解也在 feasible set 里,而且至少比 IP 的 optimal cost 更大(因为 round 之后的结果未必是 \(0,1\) 取值的,不一定是 IP 的解)。
Bound and Branch
Pure Integer Programming
本质上就是,利用 relaxed linear programming 来寻找一组 optimal solution(一般用 simplex method)\(x= (x_1,x_2,\cdots,x_n)\),其中会有若干个是非整数解,记为 \(x_{m1},x_{m2},\cdots,x_{mk}\)。此时可以对每个 \(x_{mi}\) 是向上 round 还是向下 round 做一个分割,就回到了 seperating hyperplane theorem。这样就得到了一个 tree,它的每一组分叉都多加了一个条件,解出所有分叉上点的解即可。
来个示意图,我也不知道为什么这个图在书上就是颈椎病图,凑合看吧(
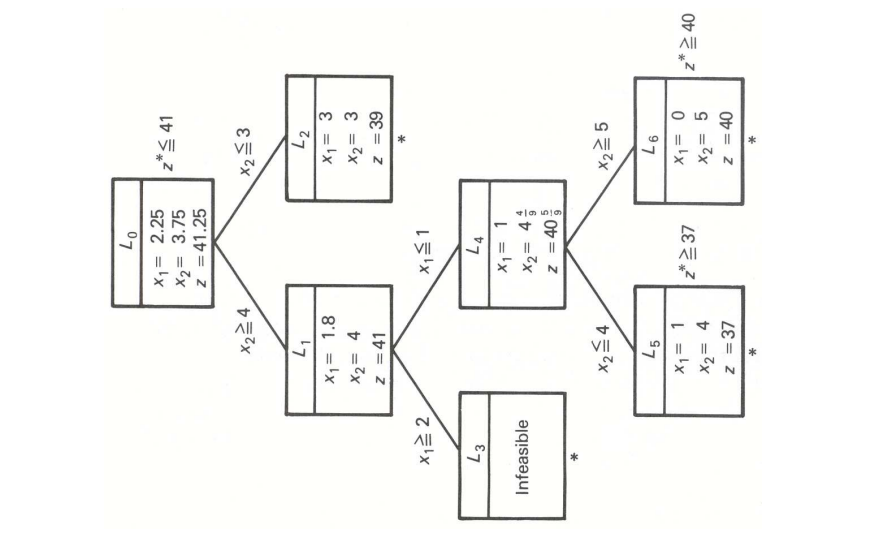
某种程度上来说和 ellipsoid method 非常相似,都是在原条件的基础上继续用 cutting plane 加条件然后继续往下解。所以说需要考虑的问题也是相似的,也即算法何时终止、time usage 如何、这棵树上的 optimal solution 是否就是真正的 optimal solution(只是在对每个非整数变量做 round,听起来不是特别靠谱)。特别地,还有树上所有的分支应该以什么样的顺序求解才最优、能否中途去掉一些 inactive 的分支来保证计算量最小。
首先观察到所有的 \(c_i\) 都是正的(如果不是正的请把 \(x_i\) 换成 \((1-y_i)\)),所以可以用 dual problem 来解
但总觉得没啥必要计算得到的最初的 \(L_0\) 的 optimal cost 记为 \(\bar z\),这样这棵树上的每一个 optimal cost 都不会大于 \(\bar z\)。
在计算的过程中,如果已经有某个 subproblem 得到了 integer solution 和相应的 optimal cost \(z^*\),则如果在其他 active subproblem with fractional solution 中得到了更小的 optimal cost \(z \leq z^*\),则说明无论如何分划,这一 active subproblem 所对应的平面区域上都不可能找到 optimal cost,直接将其置为 inactive 即可。
换言之,在找到一个 optimal cost 为 \(z^*\) 之后,只需要再寻找一个 optimal cost 为 \(z\),满足 \(z^* \leq z \leq \bar z\) 的整数解。这就是 bound and branch 中 bound 的来源。
Infeasible subproblem 也不需要再分划下去。
最后得到的 algorithm 大致是:
- Solve the linear relaxation of the problem. If the solution is integer, then we are done. Otherwise create two new subproblems by branching on a fractional variable.
- A subproblem is not active when any of the following occurs:
- You used the subproblem to branch on
- All variables in the solution are integer
- The subproblem is infeasible
- You can fathom the subproblem by a bounding argument
- Choose an active subproblem and branch on a fractional variable. Repeat until there are no active subproblems.
Mixed Integer Programming
Mixed integer programming 的 bound and branch 方法和上述几乎并无不同,只是每一次加条件做分枝的时候只对 integer variable 加条件,计算量会隐性地小一点。
Cutting Plane Method
我个人认为课件上说这个条件在二维条件下用比 bound and branch
简单这件事非常逆天,就,我用 bound and branch 来解 integer programming
的时候也是用画图来做的啊,谁真的拿 simplex method 解 \(2^k\) 个 linear programming
啊((
用一个例子来解释:
\[\begin{aligned}\textbf{maximize} &\quad 7x_1+ 9x_2 \\ \textbf{subject to}& \quad -x_1+3x_2 \leq 6 \\ & \quad 7x_1+x_2 \leq 35 \\ & \quad x_1,x_2 \in \mathbb N \end{aligned}\]
类似于化成 linear programming 的方法,但是相应的 slack variable 也是正整数:
\[\begin{aligned}\textbf{minimize} &\quad -7x_1- 9x_2 \\ \textbf{subject to}& \quad -x_1+3x_2+s_1=6 \\ & \quad 7x_1+x_2 +s_2= 35 \\ & \quad x_1,x_2,s_1,s_2 \in \mathbb N \end{aligned}\]
用 simplex method 得到一个最终的 full tableau(也就是无视掉上述 linear programming 的整数条件进行一个优化的做,得到 LP 对应的 optimal solution),此时的 tableau 如下所示:
| \(x_1\) | \(x_2\) | \(s_1\) | \(s_2\) | ||
|---|---|---|---|---|---|
| \(63\) | \(0\) | \(0\) | \(28/11\) | \(15/11\) | |
| \(x_2\) | \(7/2\) | \(0\) | \(1\) | \(7/22\) | \(1/22\) |
| \(x_1\) | \(9/2\) | \(1\) | \(0\) | \(-1/22\) | \(3/22\) |
也就是说在计算中最后得到的 constraints 为:
\[\begin{aligned} & x_2+7/22 s_1+ 1/22s_2=7/2 \\ & x_1 - 1/22 s_1+ 3/22 s_2= 9/2 \end{aligned}\]
把所有的整数部分放在左边,分数 round 到最小放在右边(注意要让右边所有 variable 的系数为负,且绝对值小于 \(1\),这样才能往后加 constraints):
\[\begin{aligned} & x_2-3 = 1/2-7/22s_1-1/22s_2 \\ &x_1 - s_1-4 =1/2-21/22s_1-3/22s_2 \end{aligned}\]
这给出了新的 constraints :
\[\begin{aligned}& 1/2-7/22s_1-1/22s_2 \leq 0 \\ & 1/2 - 21/22s_1-3/22s_2 \leq 0 \end{aligned}\]
Solution to 0-1 Knapsack Problem
这 PPT 上怎么说是一个一个试啊(挠头
举个例子先:
\[\begin{aligned} \textbf{maximize} \quad & z=3x_1-2x_2+5x_3 \\ \textbf{subject to} \quad & x_1+2x_2-x_3 \leq 2 \\ & x_2+4x_2+x_3 \leq 4 \\& x_2+x_3 \leq 3 \\ &4x_2+x_3 \leq 6 \\ & x_1,x_2,x_3 \in \{0,1\} \end{aligned}\]
当然可以把 \((x_1,x_2,x_3)\) 按照 \(000,001,010,011,100,101,110,111\) 来逐个尝试,稍微简化一下的话可以考虑
\[\begin{aligned} \textbf{maximize} \quad & z=5x_3 +3x_1-2x_2\\ \textbf{subject to} \quad & x_1+2x_2-x_3 \leq 2 \\ & x_2+4x_2+x_3 \leq 4 \\& x_2+x_3 \leq 3 \\ &4x_2+x_3 \leq 6 \\ & x_1,x_2,x_3 \in \{0,1\} \end{aligned}\]
把 cost function 中系数最大的 \(5x_3\) 提到最前面,如果能够达到最大则 \(x_3=1\) 的情况较为有利。我们发现 \((x_1,x_2,x_3) = (0,0,1)\) 能够符合 constraints 而且 cost 为 \(5\),因此其后讨论其他取值时 cost 小于 \(5\) 的可以无需带入检查 constraints,直接舍去。

