《概率论 (1)》课程第一次
bonus。一个略长的证明,我使用的证明框架来自这里。感觉挺有意思,发出来水一篇留作纪念(,毕竟博客的数学
tag 下面几乎全是统计,成何体统。
本文发布时已过本次加分作业设定的截止时间。
证完了才知道 Kai Lai Chung 附录和 lzx 的课程笔记里都有提示是正常的吗(,有的人上课是真的一点都不听啊(
证明使用英文完成,我的英语全盛期水平高考才考了
135(虽然是地狱难度的上海英语),可想而知有多烂。
Get started!
In the following, \(\Omega\) is a set. Whenever a union of sets is denoted \(\uplus\) as opposed to \(\cup\), it indicates that the sets involved are pairwise disjoint.
Definition 1 (semi-ring)
Definition 1 (semi-ring):
A semi-ring on \(\Omega\) is a subset \(\mathcal S\) of the power set \(P(\Omega)\) with the following properties:
- \(\emptyset \in \mathcal S\)
- \(A,B \in \mathcal S \Rightarrow A\cup B \in \mathcal S\)
- \(A,B \in \mathcal S \Rightarrow \exists n \geq 0, \exists A_i \in \mathcal S: A \setminus B = \uplus_{i=1} ^n A_i\)
Definition 2 (ring)
Definition 2 (ring):
A ring on \(\Omega\) is a subset \(\mathcal R\) of the power set \(P(\Omega)\) with the following properties:
- \(\emptyset \in \mathcal R\)
- \(A,B \in \mathcal R \Rightarrow A \cup B \in \mathcal R\)
- \(A , B \in \mathcal R \Rightarrow A \setminus B \in \mathcal R\)
Remark 1:
\(A \cup B = A\setminus (A \setminus B)\) and therefore that a ring is closed under pairwise intersection.
A ring on \(\Omega\) is also a semi-ring on \(\Omega\).
Let \((\mathcal R_i ) _{i \in I}\) be an arbitrary family of rings on \(\Omega\), with \(I \neq \emptyset\). Then \(\mathcal R \triangleq \cap_{i \in I} \mathcal R_i\) is also a ring on \(\Omega\).
These properties are trivial.
Definition 3 (ring generated by set)
Definition 3 (ring generated by set):
Let \(\mathcal A\) be a subset of the power set \(P(\Omega)\). Define $ R (A) { R$ is ring on \(\Omega : \mathcal A \subset \mathcal R\}\).
It's easy to show that \(P(\Omega)\) is a ring on \(\Omega\), and that \(R(\mathcal A)\) is not empty. Define \(\mathcal R(\mathcal A) \triangleq \cap _{\mathcal R \in R(\mathcal A)} \mathcal R\) as the ring generated by \(\mathcal A\).
Remark 2:
- In the definition above, we should show that \(\mathcal R(\mathcal A)\) is a ring on \(\Omega\) cause it's defined as the intersections of all rings in \(R(\mathcal A)\).
- \(\mathcal A \subseteq \mathcal R(\mathcal A)\).
Proposition 1 (the way to generate a ring by a semi-ring)
Proposition 1 (the way to generate a ring by a semi-ring):
Let \(S\) be a semi-ring on \(\Omega\). Define the set \(\mathcal R\) of all finite unions of pairwise disjoint elements of \(\mathcal S\), i.e.
\[\mathcal R \triangleq \lbrace A:A = \uplus_{i=1} ^n A_i ,A_i \in \mathcal S,n\in \mathbb Z+ \rbrace\]
(where if \(n=0\), the corresponding union is empty, i.e. \(\emptyset \in \mathcal R\)). Then \(\mathcal R = \mathcal R(\mathcal S)\).
Proof:
First to prove that \(R\) is a ring. Let \(A = \uplus _{i=1} ^n A_i\) and \(B= \uplus _{j=1} ^p B_j \in \mathcal R\):
- \(A \cap B = \uplus _{i,j} (A_i \cap B_j)\) and that \(\mathcal R\) is closed under pairwise intersection.
- If \(p \geq 1\), then \(A\setminus B = \cap_{j=1} ^p (\uplus _{i=1} ^n (A_i \setminus B_j))\), and that \(\mathcal R\) is closed under set difference.
- \(A \cup B = (A\setminus B) \uplus B\), and that \(\mathcal R\) is a ring on \(\Omega\).
Then to prove that \(\mathcal R\) is the minimal ring that contains \(\mathcal S\), which is trivial.
So \(\mathcal R(\mathcal S)\) is indeed the ring generated by the semi-ring \(\mathcal S\), now we have the way to generate a ring from a semi-ring.
Remark 3 (Another way to generate a ring by a semi-ring):
Everything being as before, define: \(\mathcal R ' \triangleq \lbrace A:A = \cup_{i=1} ^n A_i,A_i \in S,n\in \mathbb Z+ \rbrace\). We don't require the sets involved in the union to be pairwise disjoint. Using the fact that the ring \(\mathcal R\) is closed under finite unoin, then \(\mathcal R' \subseteq \mathcal R\) while \(\mathcal R\) is the minimal ring that contains \(\mathcal S\), thus \(\mathcal R' = \mathcal R = \mathcal R (\mathcal S)\).
Definition 4 (measure on set)
Definition 4 (measure on set):
Let \(\mathcal A \subseteq P(\Omega)\) with \(\emptyset \in \mathcal A\). We call measure on \(\mathcal A\), any map \(\mu: \mathcal A \to [0,+\infty]\) with the following properties:
- \(\mu(\emptyset) = 0\)
- \(A \in \mathcal A,A_n \in \mathcal A\) and \(A = \uplus _{n=1} ^{+\infty} A_n \Rightarrow \mu(A) = \Sigma_{i=1} ^{+\infty} \mu (A_n)\) (which is called countable additivity)
While $A $ is a \(\sigma-\)algebra on \(\Omega\), the second property can be replaced by:
- \(A_n \in \mathcal A\) and \(A = \uplus _{n=1} ^{+\infty} A_n \Rightarrow \mu(A) = \Sigma_{i=1} ^{+\infty} \mu (A_n)\)
Remark 4:
We don't require the set $A $ is a \(\sigma -\)algebra on \(\Omega\). If \(A,B \in \mathcal A\), \(A \subseteq B\) and \(B \setminus A \in \mathcal A\), then \(\mu(A) \leq \mu(B)\). The proof is trivial.
Proposition 2 (measure extended from semi-ring to ring)
Proposition 2 (measure extended from semi-ring to ring):
Let \(\mathcal S\) be a semi-ring on \(\Omega\), and \(\mu : \mathcal S \to [0,+\infty]\) be a measure on \(\mathcal S\). There exists an extension of \(\mu\) on \(\mathcal R(\mathcal S)\), i.e. a measure \(\bar{\mu}: \mathcal R (\mathcal S) \to [0,+\infty]\) such that \(\bar{\mu}|_{\mathcal S } = \mu\).
Proof:
Let \(A\) be an element of \(\mathcal R =\mathcal R(\mathcal S)\) with representation \(A = \uplus _{i=1} ^n A_i\) as a finite union of pairwise disjoint elements of \(\mathcal S\). Define \(\bar{\mu} (A) = \Sigma_{i=1} ^n \mu(A_i)\) as the extended measure on ring \(\mathcal R\). Then check it's well-defined, derived from \(\mathcal S\), and is a measure.
Let \(A \in \mathcal R(\mathcal S)\), \(A = \uplus _{i=1} ^n A_i = \uplus _{j=1} ^p B_j\), show that \(\bar{\mu} (A) = \Sigma_{i=1} ^n \mu(A_i)=\Sigma_{j=1} ^m \mu(B_j)\).
For \(i=1,2,...,n\), \(\mu (A_i) = \Sigma_{j=1} ^p \mu(A_i \cap B_j)\), for \(j=1,2,...,p\), \(\mu(B_j) = \Sigma_{i=1} ^n \mu(A_i \cap B_j)\).
Then \(\Sigma_{i=1} ^n \mu(A_i)= \Sigma_{i=1} ^n \Sigma_{j=1} ^p \mu(A_i \cap B_j)= \Sigma_{j=1} ^p \Sigma_{i=1} ^n \mu(A_i \cap B_j)= \Sigma_{j=1} ^m \mu(B_j)\), so the map \(\bar{\mu} :\mathcal R (\mathcal S) \to [0,+\infty]\) is well-defined.
Easy to show that \(\bar{\mu}|_{\mathcal S } = \mu\).
Suppose that \((A_n)_{n \geq 1}\) is a sequence of pairwise disjoint elements of \(\mathcal R (\mathcal S)\), each \(A_n\) have the representation \(A_n = \uplus _{k=1} ^{p_n} A_n ^k , n \geq 1\) as a finite union of disjoint elements of \(\mathcal S\).
Suppose moreover $A = _{n=1} ^{+} A_n $ is an element of \(\mathcal R(\mathcal S)\) with representation \(A = \uplus_{j=1} ^p B_j\), as a finite union of pairwise disjoint elements of \(\mathcal S\).
We want to show that \(\bar{\mu} (A) = \Sigma_{n=1} ^{\infty} \bar{\mu} (A_n)\), then \(\bar{\mu}\) meets the property of countable additivity, thus it's a measure on \(\mathcal R(\mathcal S)\).According to the definition of \(\bar{\mu}\), \(\bar{\mu}(A) = \Sigma_{j=1}^p \mu( B_j)\).
For each \(j=1,2,...,p\), \(B_j = \cup_{n=1} ^{+\infty} \cup_{k=1}^{p_n} (A_n ^k \cap B_j) = \uplus_{m=1} ^{+\infty} C_m\), while for \(m=1,2,...,+\infty\), \(C_m = \uplus _{k=1}^{p_n} (A_n ^k \cap B_j)\) is a union of disjoint pairwise elements in \(\mathcal S\), then \(C_m \in \mathcal S\).
According to the definition of \(\bar{\mu}\), \(\mu(C_m) = \Sigma_{k=1} ^{p_n} \mu(A_n ^k \cap B_j)\), thus \(\mu(B_j) = \Sigma_{m=1} ^{+\infty} \mu(C_m) = \Sigma_{n=1} ^{+\infty}\Sigma_{k=1} ^{p_n} \mu(A_n ^k \cap B_j)\).
On the other hand, \(A_n ^k = A_n ^k \cap A = \uplus_{j=1} ^p (A_n ^k \cap B_j)\), thus \(\bar{\mu}(A_n ^k) = \mu(A_n ^k) = \Sigma_{j=1} ^p \mu(A_n ^k \cap B_j)\). While $A_n = _{k=1} ^{p_n} A_n ^k $, we know that \(\bar{\mu} (A_n)= \Sigma_{k=1}^ {p_n} \bar{\mu}(A_n ^k) = \Sigma_{k=1}^ {p_n} \Sigma_{j=1} ^p \mu(A_n ^k \cap B_j)\).
After all, ${}(A) = {j=1} ^p (B_j) = {j=1} ^p {n=1} ^{+}{k=1} ^{p_n} (A_n ^k B_j) = {n=1} ^{+} {k=1}^ {p_n} {j=1} ^p (A_n ^k B_j) = {n=1} ^{+}{}(A_n) $, which indicates that \(\bar{\mu}\) is a measure on \(\mathcal R(\mathcal S)\).
Thus \(\bar{\mu}\) is a extended measure on the ring \(\mathcal R (\mathcal S)\), and is extended from the semi-ring \(\mathcal S\).
Proposition 3 (Uniqueness of the extension \(\bar{\mu}\))
Proposition 3 (Uniqueness of the extension \(\bar{\mu}\))
Let \(\mathcal S\) be a semi-ring on \(\Omega\), and \(\mu : \mathcal S \to [0,+\infty]\) be a measure on \(\mathcal S\). There exists an unique extension of \(\mu\) on \(\mathcal R(\mathcal S)\), i.e. a measure \(\bar{\mu}: \mathcal R (\mathcal S) \to [0,+\infty]\) such that \(\bar{\mu}|_{\mathcal S } = \mu\).
Proof:
We just prove the uniqueness of the structure of \(\bar{\mu}\) in proposition 2.
Take \(\bar{\mu} : \mathcal R (\mathcal S) \to [0,+\infty]\) as defined in proposition 2, we proved that \(\bar{\mu}\) is indeed a measure on the ring \(\mathcal R (\mathcal S)\). Let \(\mu '\) be another measure extended from \(\mathcal S\).
For each \(A \in \mathcal R(\mathcal S)\), \(A\) has a representation \(A = \uplus_{i=1} ^n A_i\) as a finite union of pairwise disjoint elements in \(\mathcal S\). According to the definition, \(\mu'(A) = \Sigma_{i=1} ^n \mu '(A_i) = \mu(A_i) = \Sigma_{i=1}^n \bar{\mu}(A_i) = \bar{\mu}(A)\). This being true for each \(A \in \mathcal R(\mathcal S)\), then the extension is unique.
Definition 5 (outer-measure)
Definition 5 (outer-measure):
We define an outer-measure on \(\Omega\) as being any map \(\mu^*: P(\Omega) \to [0,+\infty]\) with the following properties:
- \(\mu ^*(\emptyset) = 0\)
- \(A \subseteq B \Rightarrow \mu^*(A)\leq \mu^*(B)\)
- \(\mu^*(\cup_{i=1} ^{+\infty} A_n) \leq \Sigma_{i=1}^{+\infty} \mu^*(A_n)\)
Remark 5:
According to the third property of outer-measure, \(\mu^*(A \cup B) \leq \mu^*(A) +\mu^*(B)\) where \(\mu ^*\) is an outer-measure on \(\Omega\) and \(A,B \subseteq \Omega\).
Definition 6 (the \(\sigma-\)algebra associated with outer-measure)
Definition 6 (the \(\sigma-\)algebra associated with outer-measure):
Let \(\mu^*\) be an outer-measure on \(\Omega\). We define:
\[\Sigma(\mu ^*) \triangleq \lbrace A \subseteq \Omega: \mu^*(T) = \mu^*(T \cap A) + \mu^*(T \cap A^C), \forall T \subseteq \Omega \rbrace\]
We call \(\Sigma(\mu^*)\) the \(\sigma-\)algebra associated with the outer-measure \(\mu^*\). (The fact \(\Sigma(\mu^*)\) is a \(\sigma-\)algebra remains to be proved)
Proposition 4 (the \(\sigma-\)algebra associated with outer-measure)
Proposition 4 (the \(\sigma-\)algebra associated with outer-measure):
Let \(\mu^*\) be an outer-measure on \(\Omega\). Let \(\Sigma = \Sigma(\mu^*)\) be the \(\sigma-\)algebra associated with \(\mu^*\). \(\Sigma\) is indeed a \(\sigma-\)algebra.
Proof:
Let \(A,B \in \Sigma\) and \(T\subseteq \Omega\). First of all, \(\Omega,\emptyset \in \Sigma(\mu^*)\) thus \(\Sigma(\mu^*)\) is non-empty.
For \(A \in \Sigma\), there is $^(T) = ^(T A) + ^(T A^C)= ^(T A^C)+ ^*(T A) $ thus \(A^C \in \Omega\).
Note that \(T\cap A^C = T \cap (A\cap B)^C \cap A^C\), \(T\cap A\cap B^C = T\cap (A\cap B)^C \cap A\), then
\[\mu^*(T\cap A^C) +\mu^*(T\cap A\cap B^C) = \mu^*(T \cap (A\cap B)^C \cap A^C) + \mu^*(T\cap (A\cap B)^C \cap A) = \mu^*(T\cap(A\cap B)^C)\]
Addint \(\mu^*(T\cap (A\cap B))\) on both sides of the equation above, there is
\[\mu^*(T) = \mu^*(T \cap(A\cap B))+\mu^*(T\cap (A\cap B)^C)\]
which suggests that \(A\cap B \in \Sigma\) when \(A ,B \in \Sigma\), we proved that intersection is closed in \(\Sigma\).
With the two properties above, it's trivial to prove that \(A\cup B\) and \(A\setminus B \in \Sigma\).
Let \((B_n)_{n \geq 1}\) be a sequence of pairwise disjoint elements of \(\Sigma\), and let \(B\triangleq \uplus_{i=1}^{+\infty} B_i\). Let \(N \geq 1\).
For each \(N \in \mathbb Z+\), there is \(\uplus_{i=1}^N B_i \in \Sigma\). Thus \(\mu^*(T\cap (\uplus_{i=1} ^N B_i)) = \Sigma_{i=1}^N \mu^*(T\cap B_n)\). According to the definition of \(B\), there is \(\uplus_{i=1} ^N B_i \subseteq B\), then \(B^C \subseteq (\uplus_{i=1}^N B_i)^C\). Thus \(T \cap B^C \subseteq T \cap (\uplus_{i=1}^N B_i)^C\).
Due to the second property of outer-measure, \(\mu^*( T \cap B^C) \leq \mu^*(T\cap (\uplus_{i=1}^N B_i)^C)\), thus there is:
\[\mu^*(T \cap B^C) +\Sigma_{i=1}^{+\infty} \mu^*(T\cap B_i) \leq \mu^*(T \cap (\uplus_{i=1}^N B_n)^C)+\Sigma_{i=1}^{+\infty} \mu^*(T\cap B_i) = \mu^*(T \cap (\uplus_{i=1}^N B_n)^C)+\mu^*(T\cap (\uplus_{i=1} ^N B_i)) = \mu^*(T)\]
cause \((\uplus_{i=1}^N B_n) \in \Sigma(\mu^*)\).
While \(\mu^*(T) \leq \mu^*(T\cap B^C) + \mu^*(T\cap B) \leq \Sigma_{i=1}^{+\infty} \mu^*(T\cap B_i) + \mu^*(T\cap B^C)\), thus \(\mu^*(T) = \mu^*(T\cap B)+ \mu(T\cap B^C)\) meets, \(B\triangleq \uplus_{i=1}^{+\infty} B_i \in \Sigma\).
All the statements above show that \(\Sigma(\mu^*)\) is a \(\sigma-\)algebra.
Proposition 5 (the measure on the \(\sigma-\)algebra \(\Sigma(\mu^*)\))
Proposition 5 (the measure on the \(\sigma-\)algebra \(\Sigma(\mu^*)\)):
Let \(\mu^*\) be an outer-measure on \(\Omega\). Let \(\Sigma = \Sigma(\mu^*)\) be the \(\sigma-\)algebra associated with \(\mu^*\). Then \(\mu^* |_{\Sigma}\) is a measure on \(\Sigma\).
Proof:
\(\mu^*\) is an outer-measure on \(\Omega\) (of course on \(\Sigma\)), then we only need to prove the countable additivity of \(\mu^*\) on \(\Sigma\).
According to the equation \(\mu^*(T \cup B) = \Sigma_{i=1}^{+\infty} \mu^*(T\cap B_i)\) in the proof of proposition 4, take \(T=B\) (cause \(\Sigma\) is a \(\sigma-\)algebra on \(\Omega\),\(B \in \Sigma\)). Thus \(\mu^*(B) = \Sigma_{i=1}^{+\infty} \mu^*( B_i)\), \(\mu^*|_{\Sigma}\) is the measure on \(\Sigma\).
Proposition 6 (the outer-measure on the set derived from a measure on the ring)
Proposition 6 (the outer-measure on the set derived from a measure on the ring):
Let \(\mathcal R\) be a ring on \(\Omega\) and \(\mu : \mathcal R \to [0,+\infty]\) be a measure on \(\mathcal R\). For all \(T \subseteq \Omega\),define:
\[\mu^*(T) \triangleq \inf \lbrace \Sigma_{n=1} ^{+\infty} \mu(A_n) , A_n \in \mathcal R , T \subseteq \cup_{n=1}^{+\infty} A_n \rbrace\]
which also means \((A_n)\) is an \(\mathcal R-\)cover of \(T\). Then \(\mu^*\) is an outer-measure on \(\Omega\), derived from the measure \(\mu\) on \(\mathcal R\), and \(\mu^* | _{\mathcal R} = \mu\).
Proof:
Take \(T=\emptyset\), \(A_n = \emptyset\) for each \(n \in \mathbb Z+\), then \((A_n)_{n\geq 1}\) is an \(\mathcal R -\)cover of \(T\). It follows that \(0 \leq \mu^*(T) \leq 0\), then \(\mu^*(T)=0\).
Let \(A \subseteq B \subseteq \Omega\). Let \((B_n)_{n\geq 1}\) be an \(\mathcal R-\)cover of \(B\), then it's also an \(\mathcal R-\)cover of \(A\).
\(\mu^*(A) \leq \Sigma_{i=1}^{+\infty} \mu(B_n)\) for each \(\mathcal R -\)cover of \(B\), then \(\mu^*(A) \leq \inf( \Sigma_{i=1}^{+\infty} \mu(B_n)) = \mu^*(B)\).
Let \((A_n)_{n \geq 1}\) be a sequence of subsets of \(\Omega\), with \(\mu^*(A_n) <+\infty\) for all \(n \geq 1\). According to the definition of \(\mu^*\), given \(\varepsilon >0\), then for all \(n \geq 1\), there exists an \(\mathcal R-\)cover \((A_n ^p)_{p\geq 1}\) of \(A_n\) such that \(\Sigma_{p=1} ^{+\infty} \mu(A_n^p) < \mu^*(A_n) +\frac{\varepsilon}{2^n}\).
For the \(\mathcal R-\)covers \(\cup_{p=1}^{+\infty} A_n^p\), \(\cup_{n=1}^{+\infty} \cup_{p=1}^{+\infty} A_n^p\) is a countable set and can be reorganized as \(\cup_{k=1} ^{+\infty} R_k = \cup_{n=1}^{+\infty} \cup_{p=1}^{+\infty} A_n^p\), while \(R_k \in \mathcal R\) for each \(k \in \mathbb Z+\). Then ${k=1} ^{+} R_k = {n=1}^{+} _{p=1}^{+} A_n^p $ is an \(\mathcal R -\)cover for \(\cup_{n=1}^{+\infty} A_n\).
According to the countable additivity of \(\mu\), \(\mu^*(\cup_{n=1}^{+\infty} A_n)\leq \mu(\cup_{n=1}^{+\infty} A_n) \leq \Sigma_{n=1}^{+\infty} \Sigma_{p=1} ^{+\infty} \mu(A_n^p)<\Sigma_{n=1} ^{+\infty} \mu^*(A_n) +\varepsilon\) holds for each \(\varepsilon >0\). Thus \(\mu^*(\cup_{i=1} ^{+\infty} A_n) \leq \Sigma_{i=1}^{+\infty} \mu^*(A_n)\) holds.
According to all the properties shown above, \(\mu^*\) is an outer-measure on \(\Omega\).
We show that $^* $ 's restriction on \(\mathcal R\) is \(\mu\) below.
Let \(A \in \mathcal R\), \((A_n)_{n \geq 1}\) be an \(\mathcal R-\)cover of \(A\) and put \(B_1 = A_1 \cap A\), and \(B_{n+1} \triangleq (A_{n+1}\cap A) \setminus ((A_1 \cap A) \cup ...\cup (A_n \cap A) )\). Thus, \((B_n)_{n \geq 1}\) is a sequence of pairwise disjoint elements in \(\mathcal R\), and \(A = \uplus_{n=1} ^{+\infty} B_n\).
It's trivial that \(\mu^*(A) \leq \mu(A)\) cause \(A\) is an \(\mathcal R-\)cover of itself.On the other hand, $(A) = {i=1} ^{+} (B_i ) {i=1} ^{+} (A_i) $ holds for each \(\mathcal R-\)cover \((A_n)_{n\geq 1}\) for \(A\). Thus \(\mu(A) \leq \inf(\Sigma_{i=1} ^{+\infty} \mu(A_i)) = \mu ^*(A)\), the equality \(\mu^*(A) = \mu(A)\) holds.
This being true for all \(A \in \mathcal R\), we have proved that \(\mu ^*| _{\mathcal R} = \mu\).
Proposition 7 (the \(\sigma-\)extension of a ring and its measure)
Proposition 7 (the \(\sigma-\)extension of a ring and its measure):
Let \(\mathcal R\) be a ring on \(\Omega\) and \(\mu : \mathcal R \to [0,+\infty]\) be a measure on \(\mathcal R\). Define \(\mu^*\) as the outer-measure derived from \(\mu\) in proposition 6. Then the \(\sigma-\)extension \(\sigma(\mathcal R)\) of \(\mathcal R\) is a subset of \(\Sigma(\mu^*)\), thus \(\mu^* |_{\sigma(\mathcal R)}\) is a measure on \(\sigma(\mathcal R)\).
Proof:
We want to show that \(\sigma(\mathcal R) \subseteq \Sigma(\mu^*)\). According to proposition 4, we know that \(\Sigma(\mu^*)\) is a \(\sigma-\)algebra, so we just need to show that \(\mathcal R \subseteq \Sigma(\mu^*)\).
Let \(A \in \mathcal R\) and \(T\subseteq \Omega\). According to the third property of outer measure \(\mu^*\), there is \(\mu^*(T) \leq \mu^* (T\cap A)+\mu^* (T\cap A^C)\).
Let \((T_n)_{n \geq 1}\) be an \(\mathcal R-\)cover of \(T\), then \((T_n \cap A)_{n \geq 1}\) and \((T_n \cap A^C)\) are \(\mathcal R-\)covers of \(T\cap A\) and \(T \cap A^C\) respectively. There is
\[\mu^*(T\cap A) +\mu^*(T\cap A^C)\leq \Sigma_{n=1} ^{+\infty} \mu(T_n \cap A)+ \Sigma_{n=1} ^{+\infty} \mu(T_n \cap A^C) = \Sigma_{n=1}^{+\infty}\mu(T_n)\]
holds for each \(\mathcal R-\)cover \((T_n)_{n \geq 1}\), thus \(\mu^*(T)=\inf(\Sigma_{n=1}^{+\infty}\mu(T_n)) \leq \mu^*(T\cap A) +\mu^*(T\cap A^C)\leq \mu^*(T)\), the equalty meets.Then it leads to \(\mu^*(T) = \mu^*(T\cap A)+\mu^*(T\cap A^C)\) holds for any \(T \subseteq \Omega\), thus \(A \in \Sigma(\mu^*)\).
This being true for all \(A \in \mathcal R\), thus \(\mathcal R \subseteq \Sigma(\mu^*)\).
Proposition 8 (the structure of the \(\sigma-\)extension of a semi-ring)
Proposition 8 (the structure of the \(\sigma-\)extension of a semi-ring):
Assume that \(\mathcal S\) is a semi-ring, its \(\sigma-\)extension is \(\sigma(\mathcal S)\). Then \(\sigma(\mathcal S) = \sigma(\mathcal R(\mathcal S))\).
Proof:
According to definition 3, we have \(\mathcal S \subseteq \mathcal R(\mathcal S) \subseteq \sigma(\mathcal R(\mathcal S))\), thus \(\sigma(\mathcal S) \subseteq \sigma(\mathcal R(\mathcal S))\).
Moreover, \(\mathcal R(S)\) is the set of all finite unions of elements of \(\mathcal S\), then \(\mathcal R(\mathcal S) \subseteq \sigma(\mathcal S)\). Consequently \(\sigma(\mathcal R(\mathcal S)) \subseteq \sigma(\mathcal S)\).
Finally, we have proved that \(\sigma(\mathcal S) = \sigma(\mathcal R(\mathcal S))\).
Theorem 1 (Carathéodory’s Extension Theorem)
Theorem 1 (Carathéodory’s Extension Theorem):
Assume that \(\mathcal S\) is a semi-ring, \(\mu : \mathcal S \to [0,+\infty]\) is a \(\sigma-\)additive function on \(\mathcal S\). Then:
- \(\mu\) has an extension measure \(\mu^*\) on \(\sigma(\mathcal S)\).
- If the \(\mu\) is \(\sigma-\)finite, then the extension measure is unique.
Proof:
First to show that \(\mu\) is a measure on semi-ring \(\mathcal S\).
The \(\sigma-\)additivity meets the second property of measure, so we just need to prove that \(\mu(\emptyset)=0\). Take \(A_1 \in \mathcal S\) as a non-empty set, and \(A_2 =A_3 =...=\emptyset\).
According to the \(\sigma-\)additivity of \(\mu\), there is \(\mu(\cup_{i=1}^{+\infty} A_i) = \mu(A_1) = \Sigma_{i=1} ^{+\infty} \mu(A_i)\), thus \(\mu(\emptyset) = 0\).
According to proposition 1 and 2, we can extend semi-ring \(\mathcal S\) to ring \(\mathcal R(\mathcal S)\) and extend measure \(\mu\) on \(\mathcal S\) to measure \(\bar{\mu}\) on ring \(\mathcal R(\mathcal S)\), which can keep \(\bar{\mu} | _{\mathcal S} = \mu\).
From proposition 6, we can extend the measure \(\bar{\mu}\) on ring \(\mathcal R(\mathcal S)\) to the outer-measure \(\mu^*\) on set \(\Omega\), which keeps \(\mu^*|_{\mathcal R(\mathcal S)} = \bar{\mu}\).
From proposition 4 and 5, we can find the \(\sigma-\)algebra \(\Sigma(\mu^*)\) associated with the outer-measure \(\mu^*\) on \(\Omega\). Also, the outer-measure \(\mu^*\) on \(\Omega\) is the measure on the \(\sigma-\)algebra \(\Sigma(\mu^*)\), which means $^*| _{(^*)} $ is a measure.
According to proposition 7 and 8, the \(\sigma-\)extension of the semi-ring \(\sigma(\mathcal S)=\sigma(\mathcal R(\mathcal S) )\subseteq \Sigma(\mu^*)\), and $^*| _{(S)}=^*| _{(R(S) )} $ is the measure on \(\sigma(\mathcal R(\mathcal S) )\). At the same time, \(\mu^*| _{\mathcal S} = \bar{\mu} |_{\mathcal S} = \mu\).
We have extended the semi-ring \(\mathcal S\) to the \(\sigma-\)algebra \(\sigma(\mathcal S)\), and the \(\sigma-\)additive function \(\mu\) to the measure \(\mu^*| _{\sigma(\mathcal S)}\).
As \(\mu\) is \(\sigma-\)finite and \(\mathcal S\) is a semi-ring, we have \(\Omega = \uplus_{n=1}^{+\infty} A_n\), \(A_n \in \mathcal S\) and \(\mu(A_n) <+\infty\). We want to prove that \(\mu_1\) and \(\mu_2\) are two measures on \(\sigma(\mathcal S)\) and \(\mu_1 |_{\mathcal S} = \mu_2 |_{\mathcal S} = \mu\), then \(\mu_1=\mu_2\).
Define \(\mathcal G = \lbrace A \in \sigma(\mathcal S) : \mu_1(A_n \cap A) = \mu_2(A_n \cap A),\forall n \in \mathbb Z+ \rbrace\), it's easy to show that \(\mathcal S \subseteq \mathcal G\). We'd like to show that \(\mathcal G\) is a \(\sigma-\)algebra, thus \(\sigma(\mathcal S) \subseteq \mathcal G\), then there will be \(\mu_1 | _{\sigma(\mathcal S)} = \mu_2 | _{\sigma(\mathcal S)}\), which means \(\mu_1\) and \(\mu_2\) are the same on \(\sigma(\mathcal S)\).
Suppose \(B_k \in \mathcal G\), for any \(k \in \mathbb N\) there is \(B_k \subset B_{k+1}\) and \(B_k \uparrow B\), then for each \(n\),
\[ \mu_1(B \cap A_n) = \lim _{k} \uparrow \mu_1(B_k \cap A_n) =\lim_{k} \uparrow \mu_2(B_k \cap A_n) = \mu_2(B \cap A_n)\]
thus \(B \in \mathcal G\). Similarly for \(C_k \downarrow C\),\(C_k \in \mathcal G\), there is \(C \in \mathcal G\). Then \(\mathcal G\) is closed for increasing and decreasing limits, $G $ is a monotone class.
Moreover, for \(K \in \mathcal G\), there is \(K^C \in \mathcal G\); for \(A,B \in \mathcal G\) and \(A \subset B\), there is \(B-A \in \mathcal G\); \(\Omega \in \mathcal G\). These properties indicates \(\mathcal G\) is a \(\lambda-\)system, while \(\mathcal S\) is a \(\pi-\)system and \(\mathcal S \subset \mathcal G\), thus \(\sigma(\mathcal S) \subseteq \mathcal G\). Then we've proved that \(\mu_1 | _{\sigma(\mathcal S)} = \mu_2 | _{\sigma(\mathcal S)}\), the extended measure on \(\sigma(\mathcal S)\) is unique.
Summary of the whole story
太抽象了,但我还是想把这个图发出来:
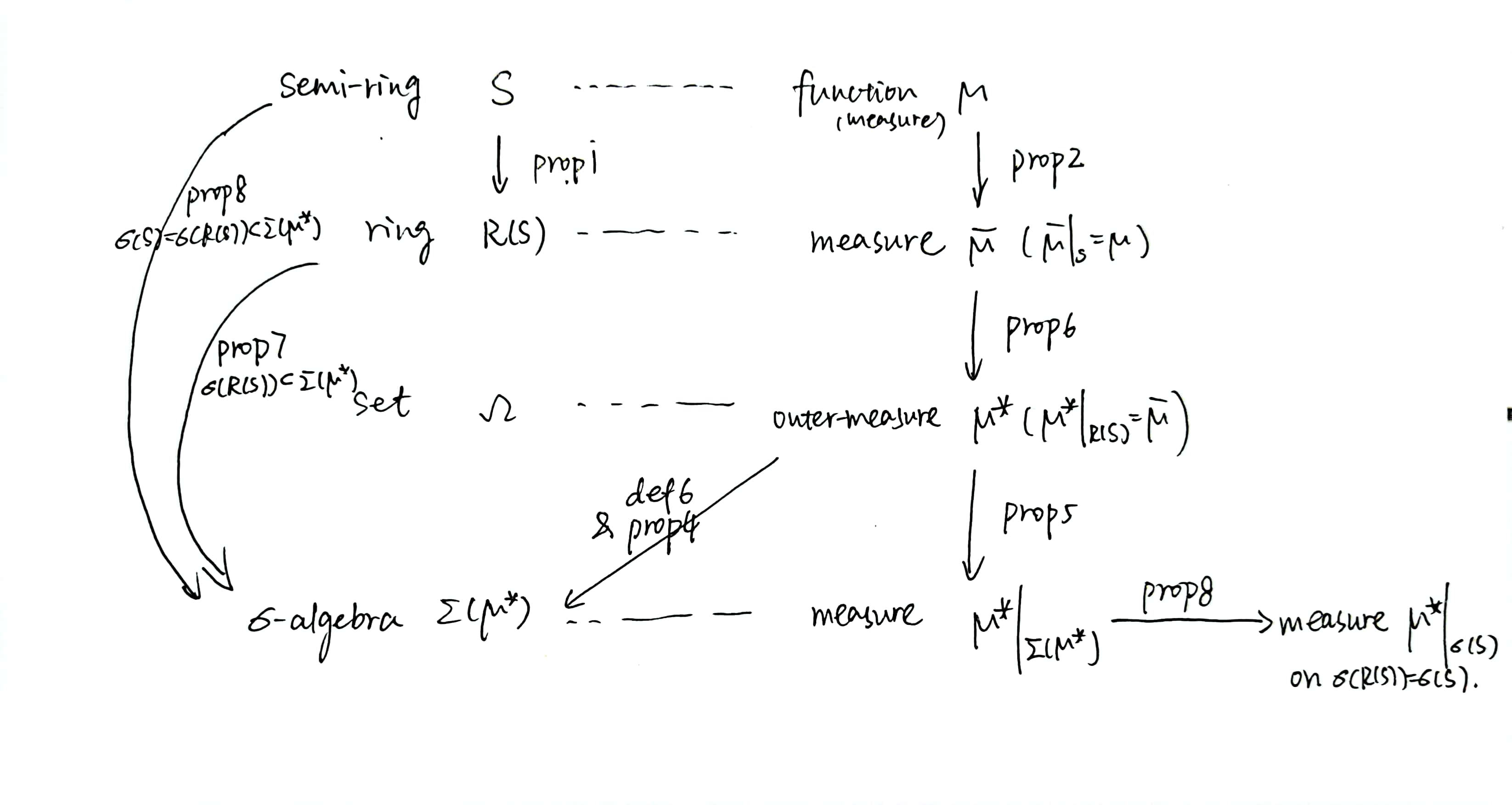
Q.E.D.!

