既然线性回归都写了,怎么能没有多元统计呢(?
其实是在课上同步写笔记体验很不错,dwl 老师的风格一如既往的稳健,课堂节奏正好。在课上敲笔记总比摸鱼好。
Lecture 1
吹水,然后讲了点基本概念。
多元数据的组织
对于多元数据,常见的形式是一个 population 中的样本个体(称为 item)有不同的项,每个 item 呈现出 p 个 variable 的取值。我们每次在 population 中抽样会取出 \(n\) 个 item,实际上获得了 \(np\) 个数据。
一般用矩阵组织二元数据,以随机变量作为列元素,把 population 中的 item 作为横行。也就是说 \(n\) 个 item 各自有 p 个随机变量项目的情况下,可以把它组织成 \(n \times p\) 尺寸的表格:
| Variable 1 | Variable 2 | ... | Variable i | ... | Variable p | |
|---|---|---|---|---|---|---|
| Item 1 | \(x_{11}\) | \(x_{12}\) | ... | \(x_{1i}\) | ... | \(x_{1p}\) |
| Item 2 | \(x_{21}\) | \(x_{22}\) | ... | \(x_{2i}\) | ... | \(x_{2p}\) |
| ... | ... | ... | ... | ... | ... | ... |
| Item j | \(x_{j1}\) | \(x_{j2}\) | ... | \(x_{ji}\) | ... | \(x_{jp}\) |
| ... | ... | ... | ... | ... | ... | ... |
| Item n | \(x_{n1}\) | \(x_{n2}\) | ... | \(x_{ni}\) | ... | \(x_{np}\) |
实际上就是一个 \(n \times p\) 大小的矩阵,每个 \(X_{ji}\) 都可以视作随机变量。因此,每一次从 population 中随机抽样出 \(n\) 个 item,都能得到一个不同的多元数据矩阵作为 observed data,在 multivariate statistics 中,observed data 一般是矩阵。
更本质地,可以把一个随机矩阵视为 \(n\) 个随机向量,每个随机向量代表了一个 item 的具体分量数据。并且可以认为这 \(n\) 个 items 是彼此独立的(\(n\) 次独立的取样),于是可以认为 joint distribution 是 \(n\) 个 PDF 之积。
描述性统计量
老生常谈了捏。对于上述的 observed data,可以纵向观察各个 variable 的性质。
列均值/sample mean :\(\bar{x_k} = \frac{1}{n} \Sigma_{i=1}^{n} x_{ik}\),\(k=1,2,...,p\)
直观来说体现了分布的位置。
列方差/sample variance :\(s_k ^2 = s_{kk} = \frac{1}{n} \Sigma_{i=1}^n (x_{ik}-\bar{x_k})^2\),\(k=1,2,...,p\)
直观来说体现了分布的分散程度。
实际上,可以看到此处列方差的系数是 \(\frac{1}{n}\) 而不是传统的 \(\frac{1}{n-1}\),这是由使用场景决定的。在统计推断中,如果需要无偏统计量则使用 \(\frac{1}{n-1}\),如果需要极大似然估计(MLE)则使用 \(\frac{1}{n}\)。尤其是样本量 \(n\) 很大的情况下,二者的差别并不大,可以不做严格的区分。
协方差,相关系数:直观上来说体现了线性相关性,相关系数为正则正相关,否则负相关,为 \(0\) 不相关。
协方差定义为 \(s_{ik} = \frac 1 n \Sigma_{j=1}^n (x_{ji} - \bar{x_i}) (x_{ji} - \bar{x_k})\),可以看到实际上 \(s_{ik} = s_{ki}\),于是协方差矩阵有
\[ \begin{bmatrix} s_{11} & s_{12} & ...& s_{1p}\\ s_{21} & s_{22} & ...& s_{2p} \\ ... & ...&...&... \\ s_{p1} & s_{p2} &...&s_{pp} \end{bmatrix}\]
的形式,这是一个对角元为正的对称矩阵。
类似地,相关系数定义为 $_{ik} = { } $ 的形式,也有对应的协方差矩阵,是一个对角元均为 \(1\) 的对称矩阵。
也可以由随机向量矩阵得到相应的 sample mean 向量和 sample variance 向量。
Mahalanobis Distance
用来判断不同 item 的 的“距离”,从来衡量两组数据的相似性。实际上不同的 variance 有不同的量纲,我们想比较不同 item 的差异,需要把 variance 的量纲“统一”来计算二者的差异。使用 Mahalanobis distance 来计算。
假设两个 item 的数据值分别是 \(P = (x_1,x_2,...,x_p),Q= (y_1,y_2,...,y_p)\),记整体 sample mean 向量为 \(\mu = (\mu_1,\mu_2,...,\mu_p)\),协方差矩阵为 \(\Sigma\)。在不同的使用场景下,Mahalanobis distance 有不同的形式,主要在以下方面处理了差异:
通过给差值除掉此维度数据的协方差,来规范尺度差异。本质上是个仿射变换。
\(d(P,Q) = \sqrt{\frac{(x_1 - y_1)^2}{s_{11} } + \frac{(x_2 - y_2)^2}{s_{22} } + ... +\frac{(x_p - y_p)^2}{s_{pp} } }\)
希望能够用二次型的形式直观表述 \(P\) 和 \(Q\),或者 \(P\) 和 \(\mu\) 之间的差异。
\(d(P,\mu) = \sqrt{(x-\mu) ^T \Sigma ^{-1} (x-\mu)}\)
\(d(P,Q) = \sqrt{(x-y)^T \Sigma^{-1} (x-y)}\)
此外还有两个结论:
设 \(Z\) 是一个随机向量,记它的均值向量为 \(\mu _Z\),协方差矩阵为 \(\Sigma _Z\),二者均有限。\(A\) 是任意的对称矩阵。于是有 \(E[Z^T AZ] = trace(A\Sigma_Z) + \mu_Z ^T A \mu_Z\)。
Proof:考虑迹的性质。\(E[Z^T AZ] = tr(E[Z^T AZ]) = E[tr(Z^TAZ)] = E[tr(AZZ^T)] = tr(E[AZZ^T]) = tr(AE[ZZ^T])\),由\(Z\) 是随机向量,\(E[ZZ^T] = (\Sigma_Z + \mu_Z ^T \mu_Z)\),故 \(tr(AE[ZZ^T]) = tr(A\Sigma_Z) + tr(A\mu_Z \mu_Z^T) = trace(A\Sigma_Z) + \mu_Z ^T A \mu_Z\)。
2-范数的期望:\(p\) 阶随机向量 \(X\) 有有限的均值向量 \(\mu\) 和协方差矩阵 \(\Sigma\),于是 \(E[|| X - \mu ||_2 ^2] = \Sigma_{i=1} ^p \sigma_{ii}\)。
Proof: 在上一个结论中取 \(A=I\),于是 \(E[|| X - \mu ||_2 ^2] = E[(X-\mu )^T I (X-\mu)] = tr(I\Sigma) = \Sigma_{i=1} ^p \sigma_{ii}\)。
Remark: 对于独立同分布的 \(X\) 和 \(Y\),有相同的均值向量和协方差矩阵,于是 \(E[||X-Y||_2^2] = 2 \Sigma _{i=1} ^p \sigma _{ii}\)。
最后来考虑 Mahalanobis distance 的期望。\(p\) 阶随机向量 \(X\) 有有限的均值向量 \(\mu\) 和协方差矩阵 \(\Sigma\),其 Mahalanobis distance 定义为 \(||X- \mu ||_\Sigma = d(X,\mu) = \sqrt{(X-\mu)^T \Sigma^{-1} (X-\mu)}\),利用上述结论则 \(E[||X- \mu ||_\Sigma ^2] = p\)。
同理,对于独立同分布的 \(X\) 和 \(Y\),有 \(E[||X-Y||_\Sigma ^2] = 2p\)。
Exploratory Data Analysis (EDA)
这个其实在线性回归课上也学过,主要讲的是数据清洗的原则和方法,也没有什么很实际的内容,感觉在扯皮。wljj 的课上比较注重解释一些看起来很炫酷的图是怎么画的,真的很应用。
这个能用 RMarkdown 写的话就好了,Typora 什么时候能支持 RMarkdown(暴论
Boxplot
1 | data = matrix(0,nrow=12,ncol=2) |
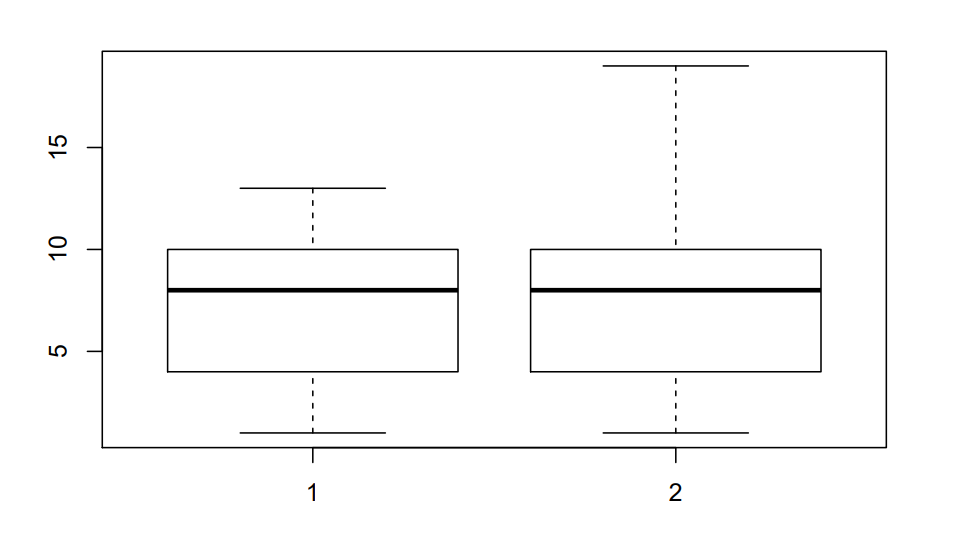
(假装在用 Rmd(
boxplot 包含了很多信息。盒子的上边表示数据中的 75% 分位数,下边表示 25% 分位数,盒子中间的线表示中位数。我们将 75% 分位数和 25% 分位数的差记作 IQR,则盒子上边距离最上方的“触角”的距离是 1.5 IQR,下边同理。
对于正态分布来说,两个触角之间的距离表示了所有正常数据的范围,离开这个范围的数据基本上是 out of 3\(\sigma\) 的,可以直观地去除 outlier。
在 R 的绘图中会将上“触角”的值定为 75% quantile + 1.5 IQR 和最大数据之间的较大值,下“触角”同理,因此在上面的这个例子里,两组数据的 25% quantile 和 75% quantile 都是相同的,绘图结果有差别。
Histogram
柱状图的宽度还是有讲究的,适当的宽度可以看出分布的形状。通用的是 \(h =( \frac{24\sqrt{\pi} } {n})^{\frac{1}{3} }\)。
1 | hist(mpg$hwy,main = "Histogram of highway miles per gallon",breaks = round(max(mpg$hwy)-min(mpg$hwy)/(24*sqrt(pi)/length(mpg$hwy))^(1/3))) |
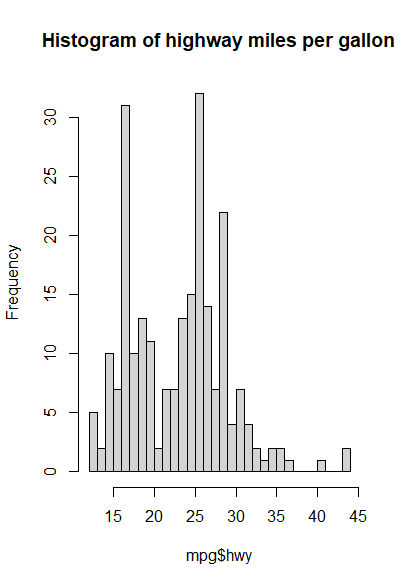
Scatter Plot
散点图有很 fancy 的版本,这里展示一些实现:
Scatter Plot
放一个我线性回归作业里的图罢。
1
2
3
4
5
6men <- c(72.5,71.5,70.5,69.5,68.5,67.5,66.5,65.5,64.5)
brothers <- c(71.1,70.2,69.6,69.5,68.7,67.7,67.0,66.5,65.6)
p = plot.default(men,brothers,xlim = c(63,73),ylim=c(65,72),main = 'Heights of men and their brothers',xlab = 'medium heights of the men',ylab = 'medium heights of the brothers',col = "blue")
abline(lm(brothers~men))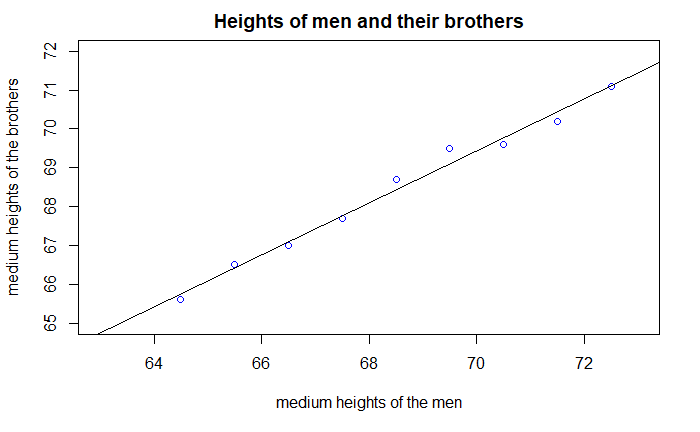
1
lm(brothers~men)
Scatter Plot Matrix
1
2
3
4library(GGally)
lizard<-read.csv('t1-3.dat',sep='',header=F)
names(lizard)<-c('mass','svl','hls')
ggpairs(lizard,title = 'scatter plot matrix of lizard')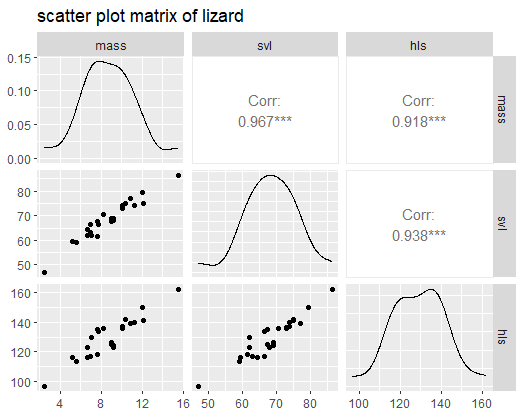
3D Scatter Plot
1
2
3library(scatterplot3d)
data(iris)
head(iris)1
scatterplot3d(iris[,1:3])
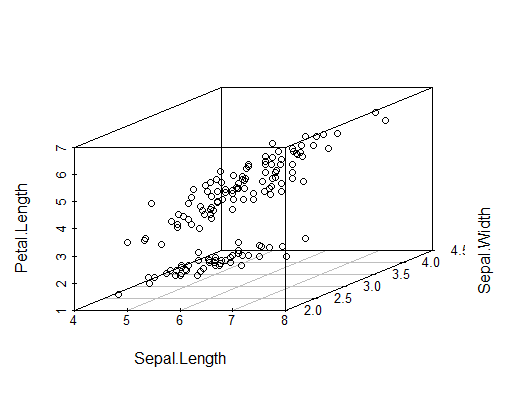
1
2
3
4colors <- c("#999999","#E69F00","#56B4E9")
colors <- colors[as.numeric(iris$Species)]
scatterplot3d(iris[,1:3],pch=16,color=colors,main='3D scatter plot of iris flower', grid=TRUE, box=TRUE, type="h")
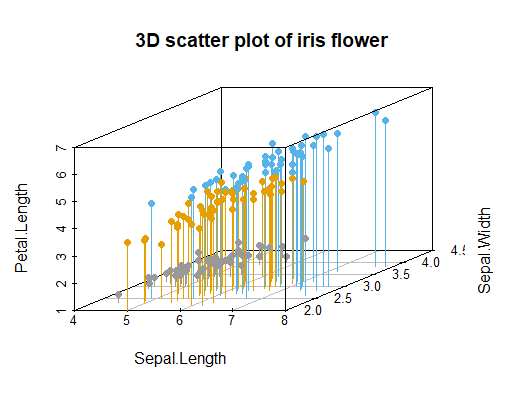
Lecture 2
介绍了一些矩阵方法,以及复习线性代数。
Linear Algebra
什么嘛,我线代学得还可以嘛(喜
矩阵分解的复习就跳过了,也就那点东西,主要是谱分解和奇异值分解。
Matrix Interpretation of Mahalanobis-distance
注意一些左乘矩阵代表的意义,比如在 Mahalanobis 距离中常用的处理方式是旋转和伸缩,二者分别可以左乘一个正交矩阵/对角矩阵来完成。
因此,回忆一下 Mahalanobis 距离的表达式 \(d(P,Q) = \sqrt{(x-y)^T \Sigma^{-1} (x-y)}\),其中要求 \(\Sigma\) 是一个对称正定矩阵,可以分解为 \(\Sigma = P AP^T\) 的形式,其中 \(P\) 是正交矩阵,\(A\) 是特征值对角矩阵。
Matrix Inequality
Extended Cauchy-Schwartz Inequality:对于两个 \(p \times 1\) 大小的向量 \(b,d\),任意的 \(B\) 满足是对称正定矩阵,于是有
\[(b^T d)^2 \leq (b^T Bb)(d B^{-1} d)\],
等号成立当且仅当 \(b=cB^{-1} d\),\(c\) 是常数。
Proof(证明摘自 Vica's Blog):注意到
\[\boldsymbol{b}^\intercal\boldsymbol{d}=\boldsymbol{b}^\intercal\boldsymbol{I}\boldsymbol{d}=\boldsymbol{b}^\intercal\boldsymbol{B}^{1/2}\boldsymbol{B}^{-1/2}\boldsymbol{d}=(\boldsymbol{B}^{1/2}\boldsymbol{b})^\intercal(\boldsymbol{B}^{-1/2}\boldsymbol{d})\]
然后套用柯西不等式即得证。
Maximization Lemma:\(B\) 是对称正定矩阵,\(d\) 是给定的向量,于是对于任意不为零的向量 \(x\),有
\[\max _{x\neq 0} \frac{(x^T d)^2}{x^T Bx} = d^T B^{-1} d\],
取到最大值时有 \(x = c B^{-1} d\),\(c\) 是常数。
Proof:即为 Extended Cauchy-Schwartz Inequality 的变形。
描述性统计量的矩阵表示
上次说到把二维数据组织成 \(n \times p\) 尺寸的表格:
| Variable 1 | Variable 2 | ... | Variable i | ... | Variable p | |
|---|---|---|---|---|---|---|
| Item 1 | \(x_{11}\) | \(x_{12}\) | ... | \(x_{1i}\) | ... | \(x_{1p}\) |
| Item 2 | \(x_{21}\) | \(x_{22}\) | ... | \(x_{2i}\) | ... | \(x_{2p}\) |
| ... | ... | ... | ... | ... | ... | ... |
| Item j | \(x_{j1}\) | \(x_{j2}\) | ... | \(x_{ji}\) | ... | \(x_{jp}\) |
| ... | ... | ... | ... | ... | ... | ... |
| Item n | \(x_{n1}\) | \(x_{n2}\) | ... | \(x_{ni}\) | ... | \(x_{np}\) |
实际上就是一个 \(n \times p\) 大小的矩阵,记为 \(A = [y_1,y_2,...,y_p]\)。
sample mean vector 也可以写成矩阵变换的表示:$ {X} = A^T _n$,其中 \(\mathbb 1_p\) 表示 \(p\) 个分量都是 \(1\) 的向量。
covariance matrix 也可以写成矩阵表达:$ n S_p = A^T (I_n - _n _n^T) A$,事实上 \(\mathbb 1_n \mathbb 1_n ^T=\mathbb 1_{n\times n}\) 是一个分量都为 \(1\) 的矩阵。
correlation matrix 在 covariance matrix 的基础上继续做变换即可。记 $D^{ 2} = diag(,..., ) $,于是 correlation matrix 可以记为 \(R_p= D^{-\frac 1 2} S_p D^{-\frac 1 2}\)
在此基础上再定义一个 generalized sample variance,事实上是 covariance matrix 的行列式值的绝对值,也就是这个对称矩阵的全体特征值的积的绝对值。由行列式的形式可以知道它是一个和各个 covariance coefficient 相关的式子,一定程度上可以反映数据的离散程度(但因为是标量,缺乏各个方向上的数据的离散情况)。例如对于二维数据(\(p=2\)),可以知道 \(|S|=s_{11} s_{22} (1- r_{12}^2)\)。
另一个常用的表示是 covariance matrix 的迹,也即这个对称矩阵的全体特征值的和。
Lecture 3
今天介绍多元正态分布。
多元正态分布
多元正态分布的概率密度形式和一元是完全类似的:
\[f(x) = \frac{1}{(2\pi) ^{p/2} |\Sigma |^{1/2}} exp(-\frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2})\]
其中,\(\mu\) 是 \(x\) 的均值,\(\Sigma\) 是 \(x\) 的协方差矩阵,这是一个正定矩阵。
先把二元的情况拿出来观察,\(p=2\),于是有 \(f(x) = \frac{1}{2\pi |\Sigma|^{1/2}} exp(-\frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2})\)。其中有
\[\mu = \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} = \begin{bmatrix} E(X_1) \\ E(X_2) \end{bmatrix}, \Sigma = \begin{bmatrix} Var{X_1} & Cov(X_1,X_2) \\ Cov(X_1,X_2) & Var(X_2)\end{bmatrix}\]
我们想对 \(\mu\) 和 \(\Sigma\) 做一些估计,回顾一下统计推断里的 MLE 估计,矩估计等等方法。
补充:矩阵向量求导、期望
向量求导很熟悉了,就是 Jacobian matrix 那一套。但在多元统计里使用的求导矩阵是 Jacobian matrix 的转置。有一些看起来轻微抽象的结论:
\[\frac{\partial}{\partial x} Ax = A^T\]
\[\frac{\partial}{\partial x} x^TA = A\]
\[\frac{\partial}{\partial x} x^Tx = 2x\]
\[\frac{\partial}{\partial x} x^TAx = Ax+A^Tx\]
实际上都非常容易推导,把 \(Ax\) 视为 \(x\) 的线性变换,再对分量求导即可。
对矩阵的求导暂时只考虑对称正定的情况。
\[\frac{\partial |A|}{\partial A} = |A| A^{-1}\]
\[\frac{\partial tr(AB)}{\partial A} =B^T\]
\[\frac{\partial tr(A^{-1}B)}{\partial A} = -A^{-1}B^TA^{-1}\]
有点抽象(
对于某一个 population \(c^T X = \begin{bmatrix} c_1 & c_2 & ... &c_p \end{bmatrix} \begin{bmatrix} X_1 \\ X_2 \\...\\X_p \end{bmatrix}\), 其期望变为 \(c^T \mu\),方差变为 \(c^T \Sigma c\);
如果 \(c^TX\) 是一个 sample,同理样本均值变为 \(c^T \mu\),样本方差变为 \(c^T Sc\)。
对于两个 population \(b^TX\) 和 \(c^TX\),有 \(Cov(b^T X,c^TX) = b^TXc\)。
注意这里是对一个随机向量的 \(p\) 个分量在做线性组合,而不是对若干个随机向量的组合,期望和方差都是标量而不是向量!
多元正态分布参数估计
极大似然估计
这个我在课上自己推出来了(喜),还喜提了 dwl 老师在我身边叫我名字 + 纠正书写,她居然还记得我,但想起来我开摆的初概,真是又开心又尴尬(。结论是:
对于 \(X_1,X_2,...,X_n\) i.i.d. \(\sim N_p (\mu,\Sigma)\),参数 \(\mu\) 和 \(\Sigma\) 的极大似然估计是:
\[ \hat{\mu}_{MLE} = \bar{X}\]
\[\hat{\Sigma}_{MLE} = \frac{1}{n} \Sigma_{i=1} ^n (X_j - \bar{X})(X_j - \bar{X})^T\]
无偏估计
首先考虑样本方差为 \(S = \frac{1}{n-1} \Sigma_{i=1} ^n (X_j - \bar{X})(X_j - \bar{X})^T = \frac{n}{n-1} \hat{\Sigma}_{MLE}\),它是 \(\Sigma\) 的无偏估计;\(\mu\) 的无偏估计显然是 \(\bar{X}\)。
事实上还有性质:\(Cov(\bar{X}) = \frac 1 n \Sigma\);\(S\) 和 \(\bar{X}\) 互相独立,且是一组充分统计量(用因子分解定理简单看一下)。
多元正态分布的性质
\(X \sim N_p(\mu , \Sigma) \iff a^TX \sim N(a^T\mu,a^T\Sigma a)\) 对任意的 \(a \in \mathbb R^p\) 成立。
\(X\sim N_p(\mu ,\Sigma) \iff AX+d \sim N_p(A\mu +d , A\Sigma A^T)\) 对任意的 \(d\in \mathbb R^p\) 成立。
对于特定的 \(N_p(\mu , \Sigma)\),我们可以用 \(p\) 个标准正态分布捏出来。对于任意的 \(Z_1,Z_2,...,Z_p\) i.i.d. \(\sim N(0,1)\),记 \(Z=(Z_1,Z_2,...,Z_p)^T\)。对任意的对称正定矩阵 \(\Sigma\) 和实向量 \(\mu \in \mathbb R^p\),有 \(X = \mu + \Sigma^{\frac 1 2} Z \sim N_p(\mu,\Sigma)\)。
对于满足多元正态分布的 \(X = (X_1,X_2,...,X_p)^T \sim N_p(\mu ,\Sigma)\),我们可以根据 \(\mu\),\(\Sigma\) 的信息找到任意一组 \((X_{i1},X_{i2},...,X_{ij})\) 的期望和方差,也可以通过协方差矩阵得到任意一对 \((X_i,X_j)\) 之间的独立性关系(注意对于正态分布,独立和不相关是等价的,对于其他分布不能这样推理)。
然而对于相关的随机向量,例如 \(\begin{bmatrix} X_1 \\ X_2\end{bmatrix}\sim N_{q_1+q_2} (\begin{bmatrix}\mu_1 \\ \mu_2 \end{bmatrix},\begin{bmatrix} \Sigma_{11} &\Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix})\),其中 \(| \Sigma_{22}|>0\),可以看到 \(X_1,X_2\) 之间并不独立。此时我们有另一种结果: $(X_1 | X_2 = x_2) N(1 + {12} {22}^{-1} (x_2 - 2),{11} - {12 } {22}^{-1} {21}) $
Proof:(这是我写在作业里的一个方法,写个作业用蹩脚英文,现在看看绷不住了)
According to the resolution:
\[\Sigma = \begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix} = \begin{bmatrix}\Sigma_{11} - \Sigma_{12 } \Sigma_{22}^{-1} \Sigma_{21} & \Sigma _{12} \\ 0 & \Sigma_{22}\end{bmatrix} \begin{bmatrix}I &0 \\ -\Sigma_{22} ^{-1} \Sigma_{21} & I\end{bmatrix}^{-1}\]
Note that:
\((x-\mu)^T \Sigma ^{-1} (x-\mu) = \begin{bmatrix}x_1^T - \mu_1^T & x_2^T - \mu_2^T\end{bmatrix} \begin{bmatrix} I & 0 \\ -\Sigma_{22}^{-1} \Sigma_{21} & I\end{bmatrix} \begin{bmatrix}(\Sigma_{11} - \Sigma_{12 } \Sigma_{22}^{-1} \Sigma_{21})^{-1} & 0 \\ 0 & \Sigma_{22}^{-1} \end{bmatrix} \begin{bmatrix}I & -\Sigma_{12} \Sigma_{22} ^{-1} \\ 0 &I\end{bmatrix} \begin{bmatrix}x_1 - \mu_1 \\ x_2- \mu_2\end{bmatrix}\)
We can know that \((x_1^T -\mu_1^T) - (x_2^T - \mu_2^T ) \Sigma_{22}^{-1} \Sigma_{21} \sim N(0,\Sigma_{11} - \Sigma_{12 } \Sigma_{22}^{-1} \Sigma_{21})\),
so that \(X_1 \sim N(\mu_1 +\Sigma_{21} \Sigma_{22}^{-1} (x_2 - \mu_2)\),${11} - {12 } {22}^{-1} {21}) $, the conditional distribution can be derived from the distribution.
因此可以看到,即使随机向量的两部分之间有相关性,也可以进行分离。
\(X \sim N_p(\mu,\Sigma)\),于是有 \((X-\mu) ^T \Sigma^{-1}(X-\mu) \sim \chi_p ^2\)。
Proof:取 \(Z=\Sigma^{\frac 1 2} \sim N_p (0,I_p)\)。
于是 \((X-\mu) ^T \Sigma^{-1} (X-\mu) = [(X-\mu)^T \Sigma^{-\frac 1 2}] [\Sigma^{-\frac 1 2} (X-\mu)] = Z^TZ =\Sigma_{i=1} ^p Z_i ^2 \sim \chi_p ^2\)。
\(X_1,X_2,..,X_n\) 是相互独立的多元正态分布,\(X_j \sim N_p(\mu_j , \Sigma)\),记 \(V_1 = c_1X_1+c_2X_2+...+c_nX_n = c^TX\)。
- \(V_1 \sim N_p(c^T \mu , c^Tc \Sigma)\);
- 对于 \(V_2 = b_1X_1+b_2X_2+...+b_nX_n\),有 \(V_1,V_2\) 的协方差矩阵为 \(\begin{bmatrix} c^Tc\Sigma & b^Tc\Sigma \\ b^Tc\Sigma & b^Tb\Sigma \end{bmatrix}\)。
- \(V_1,V_2\) 相互独立 \(\iff b^Tc = 0\)(由上一结论直接得出)
尤其要注意此处与上一部分最后一段的关系,\(V_1,V_2\) 是在对若干随机向量做线性组合,上一部分最后一段是在对一个随机向量的全体分量做线性组合。也可以从所得结果的维数来判断。
Lecture 4
单正态分布总体的推断。
Wishart Distribution
$S = _{i=1} ^n (X_j - {X})(X_j - {X})^T $,有 \((n-1)S =\Sigma_{i=1} ^{n-1} Z_i Z_i^T \sim W_p(n-1,\Sigma)\),其中 \(Z_i \sim N_p (0,\Sigma)\)。
类似于一个 \(\chi^2\) 分布在多元分布上的推广。
对于 \(A_1 \sim W_p(m_1,\Sigma)\),\(A_2 \sim W_p(m_2,\Sigma)\) 且 \(A_1,A_2\) 相互独立,则有 \(A_1 +A_2 \sim W_p (m_1+m_2,\Sigma)\)。
对于 \(A \sim W_p(m,\Sigma)\),$C $ 是一个 \(p\times p\) 大小的可逆矩阵,则 \(C^TAC \sim W_p(m,C^T\Sigma C)\)。
注意 \(C\) 可以是 $k p $ 大小的矩阵,此时也有 \(C^TAC \sim W_k(m, C^T\Sigma C)\)。这是因为 \(A = \Sigma_{i=1}^m Z_iZ_i ^T\),其中 \(Z \sim N_p(0,\Sigma)\),于是有 \(C^TAC =\Sigma_{i=1} ^m C^TZ_i Z_i ^TC\) 且 \(C^TZ_i \sim N_k ( 0, C^T\Sigma C)\),因此 \(C^TAC \sim W_k(m,C^T\Sigma C)\)。此处尤其需要注意随机向量的维数改变为 \(k\) 维。
以上两个性质都可以轻松地通过 Wishart distribution 的构造推出。
One Sample T-test
在一元情况下有 \(\frac{\sqrt{n}(\bar{X} - \mu_0)}{\sigma} \sim N(0,1)\) 和 \(\frac{(n-1)S^2}{\sigma^2} \sim \chi_{n-1} ^2\),以及 \(\frac{\bar{X} - \mu_0}{S/\sqrt n} \sim t_{n-1}\) 和 \((\frac{\bar{X} - \mu_0}{S/\sqrt n})^2 \sim F_{1,n-1}\),这些都是假设检验中常用的检验统计量。我们希望能够推广到多元的情况。
对于一族 \(X_1,X_2,...,X_n \sim N_p(\mu , \Sigma)\),假设 \(H_0 :\mu = \mu_0 ; H_1 :\mu \neq \mu_0\)。
在 \(H_0\) 下有
\[\frac{T^2}{n-1} = \sqrt n (\bar{X} - \mu_0)^T (\Sigma (X_j - \bar X)(X_j - \bar X)^T)^{-1} \sqrt n (\bar{X} - \mu_0) = Z_1 (\Sigma_{i=1} ^n Z_iZ_i^T)^{-1}Z_i^T \sim \frac{p}{n-p} F_{p,n-p}\]
也就是说 \(\frac{n-p}{p(n-1)} T^2 \sim F_{p,n-p}\),当 \(T_0 ^2 > T^2 (\alpha) = \frac{p(n-1)}{n-p} F_{p,n-p}(\alpha)\) 时拒绝原假设。这被称为 Hotelling distribution。
对于 \(X_i \sim N_p(\mu,\Sigma)\),考虑 \(Y_i = CX_i+d\),其中 $C $ 是 \(p \times p\) 的矩阵,\(d\) 是 \(p \times 1\) 的向量。这是一族多元正态分布的线性变换。
于是有 \(\bar{Y} = C \bar{X}+d\),\(S_Y = \frac{1}{n-1}\Sigma_{i=1}^n (Y_i - \bar{Y_i})(Y_i-\bar Y_i)^T = CS_XC^T\),考虑其期望有 \(\mu _Y = C \mu +d\),在假设 \(H_0\) 下有 \(\mu_{Y,0} = C \mu_0 +d\)。于是对应的 Hotelling Statistic 是
\(\begin{aligned} T^2 _Y &= \sqrt n (\bar Y - \mu_{Y,0})^T (\Sigma (Y_i - \bar{Y})(Y_i - \bar Y)^T)^{-1} \sqrt n (\bar{Y} - \mu_{Y,0}) \\& =\sqrt n (\bar{X} - \mu_0)^T C^T C^{-T}(\Sigma (X_j - \bar X)(X_j - \bar X)^T)^{-1}C^{-1}C \sqrt n (\bar{X} - \mu_0) \\& =\sqrt n (\bar{X} - \mu_0)^T (\Sigma (X_j - \bar X)(X_j - \bar X)^T)^{-1} \sqrt n (\bar{X} - \mu_0) \\& =T^2_X \end{aligned}\)
可以看到与做线性变换之前是相同的,也即对于 \(Y_i = CX_i +d\),可以使用相同的 test statistic 进行检验。
实际上,Hotelling test 和 likelihood ratio test 是完全等价的,这个可以在一元的情况下看到,也可以推广到多元。多元情况下的 likelihood ratio 是:
\[\Lambda = (\frac{|\hat \Sigma|}{|\hat \Sigma_0|}) ^{\frac n 2}= (\frac{|\Sigma_{j=1} ^n (x_j - \bar x)(x_j - \bar x)^T|}{|\Sigma_{j=1} ^ n (x_j - \mu_0)(x_j-\mu_0)^T|})^{\frac n 2}\]
由此得到 test statistic 的另一表示,不需要对矩阵 \(S\) 求逆:
\[T^2 = (n-1) \frac{|\Sigma_{j=1} ^n (x_j - \mu_0)(x_j - \mu_0)^T|}{|\Sigma_{j=1} ^ n (x_j - \bar x)(x_j-\bar x)^T|} - (n-1)\]
Confidence Interval of \(\mu_{p \times 1}\)
Confidence Region of the Mean
已知 \(Z_1,Z_2,...,Z_n i.i.d \sim N_p(\mu,\Sigma)\),对于已有的数据 \(z_1,z_2,...,z_n\) 希望求得 \(\mu\) 的置信区间,其中 \(\mu ,\Sigma\) 均未知。在一元的情况下 (\(p=1\)) 可以使用 \(\frac{\bar Z - \mu}{s / \sqrt n} \sim t_{n-1}\) 进行估计。\(\mu\) 的 \(100(1-\alpha)\%\) 置信区间是 \((\bar Z - t_{n-1,\alpha /2} \frac{s}{\sqrt n},\bar Z +t_{n-1,\alpha /2} \frac{s}{\sqrt n})\)。
在多元情况下,有 $ T^2 F_{p,n-p}$,其中 \(T^2 = n (\bar Z - \mu)^T S^{-1} (\bar Z - \mu)\)。于是 \(\mu\) 的 \(100(1-\alpha)\%\) 置信域是满足以下条件的区域:
\[R(x) = \{\mu: n(\bar Z - \mu )^T S^{-1} (\bar Z -\mu) \leq c^2 , c^2 = T^2(\alpha) = \frac{p(n-1)}{n-p}F_{p,n-p}(\alpha) \}\]
这是一个椭圆。
Individual Coverage Intervals
接下来考虑 \(Z_1,Z_2,...,Z_n\) 的线性组合 \(a^T Z = a_1 Z_1 + ... +a_n Z_n\),我们希望估计它的均值 \(a^T \mu\),这是一个标量。
由于 \(a^T Z \sim N(a^T \mu, a^T \Sigma a)\),因此 \(a^T \mu\) 的 \(100 \% (1-\beta)\) 置信区间是 \((a^T \bar Z - t_{n-1}(\beta/2) \sqrt{a^T \frac S n a},a^T \bar Z + t_{n-1}(\beta/2) \sqrt{a^T \frac S n a})\)
以下继续考虑 \(Z_1,Z_2,...,Z_n\) 的一族共 \(m\) 个线性组合 \(a_1 ^T Z,a_2 ^T Z,...,a_m ^TZ\) 的置信区间推断。
Bonferroni's Method
对于 \(m\) 个不同的线性组合 \(a_1^TZ,a_2^TZ,...,a_m^TZ\),分别对其做置信系数为 \(\frac \alpha m\) 的置信区间,则这 \(m\) 个区间拼在一起得到的矩体就至少能够包含住真正的置信域。
也就是说,对每个 \(a_i^T\mu\) 做置信区间:\((a_i ^T\bar{X} - t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_i ^T \frac S n a_i},a_i ^T\bar{X} + t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_i ^T \frac S n a_i} )\)
拼在一起得到的矩体
\[(a_1 ^T\bar{X} - t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_1 ^T \frac S n a_1},a_1 ^T\bar{X} + t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_1 ^T \frac S n a_1} ) \times \cdots \times(a_m ^T\bar{X} - t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_m ^T \frac S n a_m},a_m ^T\bar{X} + t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_m ^T \frac S n a_m} )\]
即为一个符合条件的置信域。实际上这一置信域的置信系数比 \(\alpha\) 更大,只是一个粗略的估计。
\(T^2\) interval
事实上,对任意的线性变换 \(a^TZ\) 都存在一个统一的 simultaneous coverage interval,也称作 \(T^2\) interval,是
\((a^T \bar{X} - c\sqrt{a^T \frac S n a},a^T \bar{X} + c\sqrt{a^T \frac S n a})\),其中 \(c^2 = T^2(\alpha) = \frac{p(n-1)}{n-p} F_{p,n-p}(\alpha)\)。
这个置信域比 Bonferroni's Method 得到的置信域更大。
注意当 \(a\) 在 \(S^{-1}\bar X\) 方向上时以上区间正好是一个 \(100\%(1-\alpha)\) 的置信区间,也即这个时候区间取到最大。但这一方向会随着样本的变化而变化。
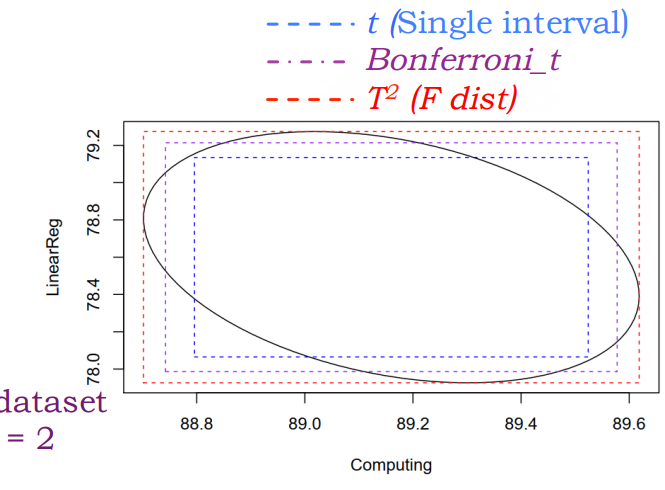
Real World(?
对 \(Z_i\) 做线性变换得到的椭圆会在形状和方向上有所变化,但与 \(T^2\) interval 得到的矩形相切。不同置信区间的覆盖面积如图所示。
Lecture 5
Two Population Test
双正态同方差总体的均值比较
两个总体中随机抽样得到的样本和相关统计量分别表示如下:
Sample \(X_{11},X_{12},...,X_{1n_1}\) \(X_{21},X_{22},...,X_{2n_2}\) Sample Mean \(\bar X_1 = \frac{1}{n_1} \Sigma_{j=1} ^{n_1} X_{1j}\) \(\bar X_2= \frac{1}{n_2} \Sigma_{j=1} ^{n_2} X_{2j}\) Sample Covariance Matrix \(S_1 = \frac{1}{n_1 -1 }\Sigma_{j=1} ^{n_1} (X_{1j} - \bar X_1)(X_{1j} - \bar X_1)^T\) \(S_2= \frac{1}{n_2 -1 }\Sigma_{j=1} ^{n_2} (X_{2j} - \bar X_2)(X_{2j} - \bar X_2)^T\) 检验前对于两个总体的假设:
- \(X_{11},X_{12},...,X_{1n_1}\) i.i.d. \(\sim N_p(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim N_p(\mu_2,\Sigma_2)\)
- 两组样本之间相互独立
- 在 \(n_1,n_2\) 较小的情况下,假设 \(\Sigma = \Sigma_1 = \Sigma_2\)
Hypothesis: \(H_0 : \mu_1 - \mu_2 = \delta_0\),\(H_1 : \mu_1 - \mu_2 \neq \delta_0\)
检验统计量的构造:
由于 \(S_{pooled} = \frac{n_1 -1 }{n_1+n_2-2}S_1 + \frac{n_2 -1}{n_1 + n_2 -2}S_2 \sim \frac{W_p(n_1 +n_2 -2,\Sigma)}{n_1+n_2-2}\),可以以此构造 Test statistic:
\[(\frac{1}{n_1} + \frac{1}{n_2})^{-1} (\bar X_1 - \bar X_2 - \delta_0)^T S_{pooled}^{-1} (\bar X_1 - \bar X_2 - \delta_0) \sim \frac{p(n_1+n_2-2)}{n_1+n_2-p-1} F_{p,n_1+n_2-p-1}\]
当 \(T_0 ^2 > \frac{p(n_1+n_2-2)}{n_1+n_2-p-1} F_{p,n_1+n_2-p-1} (\alpha)\) 时拒绝原假设。
置信区间的构造:
对于任意的线性变换 \(a^T(\mu_1 - \mu_2)\),simultaneous confidence interval 是
\[(a^T(\bar X_1 - \bar X_2) - c \sqrt{a^T (\frac{1}{n_1} + \frac{1}{n_2}) S_{pooled} a},a^T(\bar X_1 - \bar X_2) + c \sqrt{a^T (\frac{1}{n_1} + \frac{1}{n_2}) S_{pooled} a})\]
其中 \(c^2 = \frac{p(n_1+n_2 -2)}{n_1+n_2-p-1}\)。
注意到 \(a\) 的任意性,可以通过取 \(a_i=e_i\) 的方式来求得 \(\mu_1 - \mu_2\) 的各个分量的置信区间;当 \(a\) 与 \(S_{pooled}^{-1} (\bar X_1 - \bar X_2)\) 时上述置信区间的 confidence level 恰为 \(100 \% (1-\alpha)\)。
Large Sample Test
Large Sample Behavior
在大样本场景下,类似于一元的中心极限定理,我们不需要正态性也可以推出一些关于 \(\bar X,S\) 在此时的近似分布。
$X_1 , X_2 ,...,X_n $ i.i.d. 来自某一总体,其均值为 \(\mu\),协方差矩阵为 \(\Sigma\),不必要求正态分布。于是有:
- \(\sqrt n (\bar X - \mu) \sim N_p(0,\Sigma)\)
- \(n (\bar X - \mu) S^{-1} (\bar X - \mu) \sim \chi^2 _p\)
注意其中 \(S = \frac{1}{n-1} \Sigma_{i=1} ^n (X_i - \bar X)(X_i - \bar X)^T\),上述两式为近似分布,在 \(n\) 远大于 \(p\) 的条件下成立。
这是我们进行后续推断的基础。
大样本单总体均值推断
$X_1 , X_2 ,...,X_n $ i.i.d. 来自某一总体,其均值为 \(\mu\),协方差矩阵为 \(\Sigma\),不必要求正态分布。
假设 \(H_0 : \mu = \mu_0; H_1 : \mu \neq \mu_0\),于是 test statistic 是 \(n(\bar x - \mu_0)^T S^{-1} (\bar x - \mu_0 ) \sim \chi^2 _p\),当 \(T_0^2 > \chi_p ^2 (\alpha)\) 时拒绝原假设。
对于任意的线性变换 \(a^TX\),\(a^T \mu\) 的 simultaneous CI 是 \((a^T \bar X - \sqrt{\chi^2 _p (\alpha)} \sqrt{\frac{a^TSa}{n} },a^T \bar X + \sqrt{\chi^2 _p (\alpha)} \sqrt{\frac{a^TSa}{n} })\)
大样本双异方差总体均值推断
检验前对于两个总体的假设:
- \(X_{11},X_{12},...,X_{1n_1}\) i.i.d. \(\sim Population(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim Population(\mu_2,\Sigma_2)\)
- 两组样本之间相互独立
- 在 \(n_1,n_2\) 较大(均远大于 \(p\))的情况下,我们允许 \(\Sigma_1 \neq \Sigma_2\)
Hypothesis: \(H_0 :\mu_1 - \mu_2 = \delta_0; H_1 : \mu_1 - \mu_2 \neq \delta_0\)
Test statistic: \((\bar X_1 - \bar X_2 - \delta_0 )^T (\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2 )^{-1} (\bar X_1 - \bar X_2 - \delta_0) \sim ^{H_0} \chi^2 _p\),当 \(T_0 ^2 > \chi^2_p(\alpha)\) 时拒绝原假设。
标准的 \(\mu_1 - \mu_2\) 的 \(100\% (1-\alpha)\) 置信域是一个椭圆,由区域
\[\{\mu_1 -\mu_2 : ( \bar X_1 - \bar X_2 - (\mu_1 - \mu_2))^T(\frac{1}{n_1}S_1 +\frac{1}{n_2}S_2)^{-1}(\bar X_1 - \bar X_2 - (\mu_1 - \mu_2)) \leq \chi^2_p(\alpha)=c^2 \}\]
表示。
类似地考虑 \(X_1,X_2\) 的线性变换,\(a^T(\mu_1 - \mu_2)\) 的 simultaneous CI 是
\[(a^T(\bar X_1 - \bar X_2) - c \sqrt{a^T(\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2)a},a^T(\bar X_1 - \bar X_2) + c \sqrt{a^T(\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2)a} ),c^2 = \chi^2_p(\alpha)\]
大样本双总体方差推断
检验前对于两个总体的假设:
- \(X_{11},X_{12},...,X_{1n_1}\) i.i.d. \(\sim Population(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim Population(\mu_2,\Sigma_2)\)
- 两组样本之间相互独立
Hypothesis: \(H_0 : \Sigma_1 = \Sigma_2; H_1 : \Sigma_1 \neq \Sigma_2\)
Test statistic:考虑 likelihood ratio \(\Lambda = \frac{max_{\theta \in \Theta_0} L(\theta)}{max_{\theta \in \Theta} L(\theta)} = \frac{|S_1|^{n_1 /2} |S_2|^{n_2/2}}{|S_{pooled}|^{n_1+n_2-2/2}}\),自由度之差为 \(v-v_0 = df(\Theta) - df(\Theta_0)\),于是在 \(H_0\) 假设下有 \(-2 \ln \Lambda \sim \chi^2_{v-v_0}\) 是为检验统计量。
George Box 对其进行了修改,使得可以对 \(g\) 个总体进行方差推断,具体略去。
Assumption Check
类似于线性回归中所讲的内容,此处略去。
Lecture 6
关于主成分分析(Principal Component Analysis)在 population 上的理论和在 sample 上的应用。希望通过对一系列随机变量的线性变换和组合,分析维度更小的数据来达到同样的结果。
For Population
PCA 方法的具体操作
面对的问题模型可以视作:随机向量 \(X^T = [X_1 , X_2,...,X_p]\) 有 \(p \times p\) 维的协方差矩阵 \(\Sigma\) 和对应的 \(p\) 个非负特征值 \(\lambda _1 \geq \lambda_2 \geq ... \geq \lambda_p \geq 0\),分别对应单位特征向量 \(e_1,e_2,...,e_p\),这是一组正交基。
我们希望能够找出 \(Y_1, Y_2,...,Y_p\) 满足 \(Y_i = a_i ^T X\),使得 \(a_i ^T a_i =1\),\(Var(Y_i)\) 最大,且 \(Cov(Y_i, Y_j)=a_i ^T \Sigma a_j=0\)。事实上由 Rayleigh 商可以知道,只要取 \(a_i = e_i\) 就可以三个愿望一次满足(,且有 \(Var(Y_i) = \lambda_i\),证明是 trivial 的。
这个变换有一些性质:
\(\Sigma_{i=1}^p Var(X_i) = \Sigma_{i=1}^p \sigma_{ii} = trace(\Sigma) = \Sigma_{i=1}^p \lambda_i = \Sigma_{i=1}^p Var(Y_i)\)
说明 PCA 前后的信息没有损失。
可以通过 \(Var(Y_i)\) 在 \(\Sigma_{i=1} ^p Var(Y_i)\) 中的占比判断这一信息的重要程度,这一数值为 \(\frac{\lambda_i}{\lambda_1 + ... \lambda_p}\)
\(Cov(Y_i , X_j) = Cov(e_i ^T X, I_j ^T X) = e_i ^T \Sigma I_j = \lambda_i e_i^T I_j = \lambda_i e_{ij}\)
因此二者之间的相关系数为 \(\rho_{Y_i , X_j} = \frac{Cov(Y_i,X_j)}{\sqrt{Var(Y_i) Var(X_j)}} = \frac{e_{ij} \sqrt \lambda_i}{\sqrt \sigma_{ii}}, i,j = 1,2,...,p\)。
对于固定的 \(j\) 有 \(\Sigma_{i=1}^p \rho_{Y_i,X_j}^2 = 1\)。这一相关系数显示了 \(X_j\) 的方差可以被 \(Y_i\) 解释的比例。
事实上,有的时候直观显示出来 \(Y_i = e_i^TX\) 中 \(X_j\) 前系数较小,这并不说明 \(X_j\) 的影响较小,计算 \(\rho_{Y_i,X_j}\) 可能会体现出较大的相关系数,显示二者之间有较大的相关性。
正规化随机变量下的 PCA
实际使用中可能存在一些单位的变化、尺度变化导致 PCA 的系数出现不同的情况。我们讨论 standardized variable \(Z_k= \frac{(X_k - \mu_k)}{\sqrt \sigma_{kk}}, k =1,2,...,p\) 下的 PCA 变换。
事实上有 \(Z = diag(\sqrt{\sigma_{11}^{-1} },\sqrt{\sigma_{22}^{-1} },...,\sqrt{\sigma_{pp}^{-1} } ) (X-\mu)\),于是 \(Cov(Z) = diag(\sigma_{11},\sigma_{22},...,\sigma_{pp})\)。 由此即得正规化情况下的 PCA 变化的参数细节,不再赘述。
多元正态分布下的 PCA
当 \(X\sim N_p(\mu ,\Sigma)\) 时,好像下节课再讲(
For Sample
回顾一下多元情况下的样本方差:
协方差定义为 \(s_{ik} = \frac 1 n \Sigma_{j=1}^n (x_{ji} - \bar{x_i}) (x_{ji} - \bar{x_k})\),可以看到实际上 \(s_{ik} = s_{ki}\),于是协方差矩阵有
\[ \begin{bmatrix} s_{11} & s_{12} & ...& s_{1p}\\ s_{21} & s_{22} & ...& s_{2p} \\ ... & ...&...&... \\ s_{p1} & s_{p2} &...&s_{pp} \end{bmatrix}\]
的形式,这是一个对角元为正的对称矩阵。
事实上,对于已知的 \(x = [x_1,x_2,...,x_p]\),希望取 \(\hat{y_i} = \hat{e_i} ^T x = \hat e_{i1}x_1 + \hat e_{i2} x_2 + ... +\hat e_{ip} x_p\) 满足 \(\hat e_i ^T \hat e_i = 1\),$Cov(y_i , y_j) = 0 $ 对不相等的 \(i ,j\) 都成立,且 \(Var(\hat y_i) = \hat \lambda_i, i = 1,2,...,p\)。\(\hat y_i\) 称为 \(i\)-th sample principal component (score),即 sample PCs。
类似于 population 情况下的 PCA,sample PCs 有以下性质:
- \(\Sigma_{i=1} ^p Var(\hat y_i) = \Sigma_{i=1}^p s_{ii} = \Sigma_{i=1}^p \hat \lambda_i\)
- \(\rho_{\hat{y_i} ,x_k} = \frac{\hat{e}_{ik} \sqrt {\hat{\lambda}_k} }{\sqrt s_{kk} }\)
Practical Issues
在实践中求得了 PC 的表达式,还需要进行一定的取舍和判断,从而选出需要使用的值。
理论很巧妙,但我真的不想写代码实现(
How many principal components to retain
可以画一个 scree plot,值在底端且明显小的需要排除。对于 sample principal component score 且是 standardized sample 的情况下,可以选取 cutoff point 是 \(1\),舍弃所有使得 \(Var(Y_i) <1\) 的 PCs,留下的即是真正的主成分。
Check normality assumption & detect outliers
- 检验正态性可以用最大的几个 PCs
- 检验离群值可以用最小的几个 PCs
Limitations
- PCA 只使用了协方差矩阵里的值,实际上没有把数据包含的信息利用完全
- 只进行线性变换
- 很难反映变量之间的线性关系
- 对离群值敏感
后记
期中考完就退课了,于是这一篇写到 lecture 6 就烂尾了,乐(
多元问题确实太难了,我到现在绩点最低的一门数学课是微积分
A(2),意思是别的都 4.0 就它 3.6
还是五个学分(这是可以说的吗)。当时就觉得多元微积分真的好麻烦。然而多元统计难度不在多元而在统计,这属实是我没想到的。
之前在 Vincent19 主页上看到过这样一句话:
A key difference between mathematics and statistics is that the former is full of lemmas while the latter is full of dilemmas.
事实上,统计对我来说最大的困难还是面对 dilemma 应该怎么做这样的问题。半个学期下来我始终觉得如今学到的处理统计问题的方法都是原始而 trivial 的,你能想到的最容易的方法就是最好的解决方案。线性回归课堂上没有任何需要动脑超过五分钟的推导,周老师时不时说我们这个不是数学课,数学不好也不要害怕,这让我无比难受,我自己是否也有点阴暗了。然而无论是看图用眼睛做模型诊断,还是写无穷无尽却又几乎一成不变的 R code 然后在 ANOVA table 里分析数据和模型参数的细微差别,都几乎让我崩溃。多元统计时不时出现的 CI 选择和“几何直观”也一样困扰我。我想我真的不擅长处理这么具体的场景,我宁愿去读晦涩的 lemma,像解谜游戏一样,我还是只喜欢做游戏。
所以,统计中心的应统课果然还是不适合我,或许数学系的统计课会稍有不同,或许不会这么纠结现实的应用问题,但我还是厌倦了。另外,我发觉自己的分析水平也没那么差。如果不是再退线性回归的话这学期要没课上了,其实是想一起丢掉的。只能说我还是太弱了,从数学转去搞统计的同学不在少数,好像只有我这样困扰。
当时写统推笔记的时候在开头写下了“实在不行的话,(方向)该换还得换啊”这样的话,然而统推很顺利地上完了,还以为方向就这么定下来了,不用再继续颠沛流离。现在却是又一次要换掉了,再一次抛弃一切。开玩笑的,统计转概率也不算是放弃一切,不然怎么会合称“概统”呢。
我之前写“感觉自己 20th 的主题是出走”,后来觉得不是,出走会是我一生的主题,cause I have a vast, vast soul.
希望自己在概率这条路上走得远一点吧,暂时先和统计说再见了...等等还有两门课还在上呢(

