本来真没打算连载这个,结果这课居然把课程笔记算成百分制里面的 10 分(,那就写罢。
有参考 Vica Yang 的统辅笔记,JhZhang 的课堂笔记和 V1ncent19 的统辅笔记,如有引用均会在文中注明,在此向前辈表示感谢。
Lecture 1
主要是在吹水,开玩笑以及活跃气氛。正经的内容大概就一个古老的回归现象,我还没有听得很懂,麻了。
Galton's Experiment
以下全是胡说八道,不能保证完全对。
介绍正态分布的时候会有一个很经典的小球过钉板的演示实验,最后落在底部的球似乎呈现出一个正态分布。但实际上球和钉子的每次碰撞都是一个 Bernoulli 过程,过了 n 层钉板就是 n 次 Bernoulli 过程加和,可以近似为正态分布。实际上只要 n 够大,由中心极限定理任何分布的加和都可以被近似为正态分布。
但我觉得实际上小球的情况并不是独立的,毕竟过程中会有相互的碰撞,真的没问题吗(
回归现象的起源是 Galton 对于父代和子代的身高做了一个统计,发现身高远离均值的父母的后代往往身高会比他们更接近平均水平,也就是某一身高水平的父母的孩子的身高中位数作为因变量,父母身高作为自变量时,拟合出的直线的斜率小于 \(1\)。
假设不发生回归现象,则和钉板现象一样,后代的性状会逐渐分散,这被认为是一个种群稳定性状的方式。听起来很玄学,似乎也有一个稍微合理的生物学解释了,但我们希望从统计学的角度分析这件事,背后是存在数学规律的。
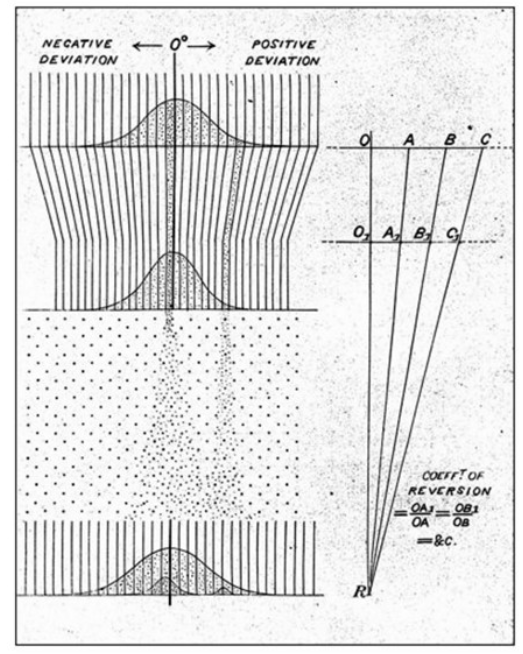
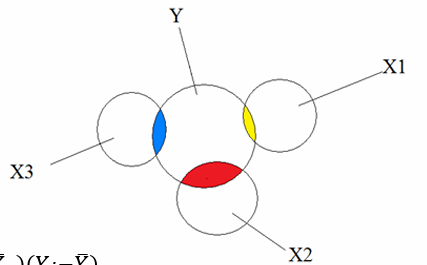
上图是课程中反复出现的一张图,对此做了很多解释。最上面的正态分布是父代的身高情况(实际上是父母身高的加权和),通过一个“倾斜槽”之后的第二个正态分布展示了子代的身高情况,比父代更加靠近中心。下方也有一个类似于钉板的装置,n 层钉板指的就是 n 代繁衍的过程,或者也可以指代一代繁衍中的其他影响身高的非基因因素,它们被视作独立同分布的,因此加和由中心极限定理可以被近似为正态分布。
图中还呈现出了父代中的一个小组“过钉板”后的结果,是一个小的正态分布。实际上子代的数据就是由一个一个小的正态分布叠加起来的,而正态分布可以线性相加,所以最后呈现出的还是正态分布。
好玄学,我也不知道我在说什么,甚至不是很确定自己理解对了没有。
Anyway,还是 think mathematically,记 \(X_i\) 为第 \(i\) 代的种群身高变化量,\(\lbrace X_i \rbrace\) 是独立同分布的。则记父代种群的随机变量为 \(F= \Sigma _{i=1} ^n X_i\),子代种群的随机变量为 \(S= \Sigma_{i=1}^nX_i\),考虑二者的相关系数:
\(\rho(F,S) = \frac{cov(F,S)}{\sqrt{Var(F)Var(S)} } = \frac{Var(F) + Cov (F,X_n)}{\sqrt{Var(F)Var(S)} } =1+\frac{cov(F,X_n)}{Var(F)}<1\),因此 \(\rho(F,X_n)<0\) 也即二者呈负相关。
一些术语
一般来说,我们把 \(X\) 作为 predictor/input/explanatory variable,把 \(Y\) 作为 response/output/dependent variable。
\(Y \sim X\) 被称为 simple regression,一元总归是简单的。
\(Y \sim X_1,X_2,...,X_p\) 称为 multiple/multivariate regression,实际上这两者是不一样的。
如果每个回归式中有超过一个 \(X\) 就称为 multiple regression,如果有多个 \(Y\) 就称为 multivariate regression,并且每个式子里只能有一个不同的 dependent variable。
还有叫做 multivariate multiple regression 的回归方法,也就是用多个 \(X\) 来预测多个 \(Y\) 的情况,每个 \(Y\) 出现在不同的式子里。
一般来说 \(Y\) 是连续型随机变量,\(X\) 可以是连续型、离散型或者分类型随机变量。有一些名词,不抄了,简单列一下:

Lecture 2
Simple Linear Regression
数据的组织和表示
Simple linear regression 的数据一般是二元数据对 \((X_i , Y_i)\),每一对数据称为一个 case。数据集记作 \((X_1,Y_1),...,(X_n,Y_n)\),其中 \(X_i\) 是 i-th observed explanatory variable,\(Y_i\) 是 i-th observed response variable。
模型的表示
\(Y_i = \beta_0 + \beta_1 X_i + \varepsilon _i\),\(\varepsilon _i\) 被称为 random error term,其中 \(\beta_0,\beta_1\) 是参数。为了简化模型便于操作,需要对 random error term 做一些假设:
- 均值为 \(E(\varepsilon_i) = 0\),方差为 \(Var(\varepsilon _i) = \sigma ^2\),注意 \(\sigma\) 是一个未知常数,也视作参数;
- 不同的 \(\varepsilon _i\) 和 \(\varepsilon _j\) 是不相关的。注意此处不需要不独立。
对于更强的模型,例如 simple linear regression model with normal error,我们直接要求 \(\varepsilon_1,...,\varepsilon_n i.i.d. \sim N(0,\sigma^2)\)(因为正态分布的不相关性和独立性等价)。这是一个很广泛的假设,但有时正态假设是明显有问题的,需要修正。
事实上,在 linear regression model 中,\(X_i\) 和 \(Y_i\) 的地位是不对等的。\(X_i\) 被视为不带随机性的常数,而 \(Y_i\) 因为 \(\varepsilon_i\) 的存在是一个随机变量,有 \(E(Y_i) = \beta_0 + \beta_1 X_i\),\(Var(Y_i)=Var(\varepsilon_i) = \sigma^2\)。因此,回归线可以视作 \((X_i, E(Y_i))\) 连成的直线,而数据点 \((X_i,Y_i)\) 分布在回归线附近。
特别地,在正态假设下, 有 \(Y_i \sim N(\beta_0 + \beta_1 X_i,\sigma^2)\),\(i=1,2,...,n\)。
参数的意义和求算
斜率 \(\beta_1\) 的意义为 \(X_i\) 增加 1 单位时 \(Y_i\) 的变化量;截距 \(\beta_0\) 的意义分两种情况解释,当 \(X_i\) 取值范围中有 \(0\) 时即为 \(X_i=0\) 时的平均响应 \(E(Y_i)\),否则截距没有意义。
Least Sum of Square 方法
求算最佳参数实际上就是求使得 sum of squared diff 最小的 \(\hat{\beta_0},\hat{\beta_1}\),从而得到 \(Y_i\) 的估计值 $= + X_i $。于是有 \(\hat{\beta_0},\hat{\beta_1} = \arg \min _{\beta_0,\beta_1} \Sigma(Y_i - \beta_0 - \beta_1X_i)^2=\arg \min _{\beta_0,\beta_1} \Sigma_{i=1 } ^n e_i ^2\)。求导即可简单地得出:
\[b_1 = \hat{\beta_1} = \frac{\Sigma_i (X_i - \bar{X})(Y_i - \bar{Y})}{\Sigma _i (X_i-\bar{X})^2}\]
\[b_0 = \hat{\beta_0} = \bar{Y} - b_1 \bar{X}\]
记残差为 \(e_i = Y_i - \hat{Y_i}= Y_i - \hat{\beta_0} - \hat{\beta_1} X_i=\beta_0 + \beta_1X_i +\varepsilon _i - \hat{\beta_0} - \hat{\beta_1}X_i \approx \varepsilon _i\) ,也即 \(e_i\) 为某一组 observed data \(Y_1,Y_2,...,Y_n\) 之下得到的残差,但绝非 \(\varepsilon _i\) 本身。残差是观测到的确定值,而 \(\varepsilon _i\) 是随机变量。
事实上求导的过程蕴含以下结论:
\[\Sigma _{i=1} ^n e_i=0\]
\[\Sigma _{i=1} ^{n} X_i e_i = 0\]
以上二式可以看做对 \(e_i\) 的线性约束,\(\lbrace e_i \rbrace\) 的自由度是 \(n-2\),互相之间不是独立的,这也是和 \(\lbrace \varepsilon _i \rbrace\) 的差别之一。由此还可以得到一些其他性质,例如回归线必过 \((\bar{X},\bar{Y})\),不在此一一列举。
以上即为参数 \(\beta_0,\beta_1\) 的估计方法。下面再考虑参数 \(\sigma\) 的估计,使用残差 \(e_1,...,e_n\) 来考虑。
取 \(\hat{\sigma ^2} = \frac{\Sigma _{i=1} ^n e_i ^2}{n-2}\)。这是因为 \(e_1,e_2,...,e_n\) 的自由度为 \(df_E = n-2\),由此考虑 sum of square \(SSE= \Sigma_{i=1} ^n (Y_i - \hat{Y_i})^2=\Sigma _{i=1} ^n e_i ^2\),定义 mean of squared errors \(MSE= \frac{SSE}{df_E} = \frac{\Sigma_{i=1}^n e_i ^2}{n-2}\) 为 \(\hat{\sigma ^2}\)。
MLE 方法
也可以用推断课上的 MLE 方法。实际上,我们想找到一个 \(\beta_0,\beta_1\) 的最佳估计,还可以使用 MLE 方法进行估计。
在正态假设下,我们可以将 \(n\) 组数据视作 \(n\) 个互相独立的随机变量,取使得其likelihood function 最大的一组 \(\beta_0,\beta_1,\sigma^2\) 作为估计量。likelihood function 即为 \(f(y_1,y_2,...,y_n) = f_1(y_1)...f_n(y_n)\),得到的 estimator 中 \(\hat{\beta_0},\hat{\beta_1}\) 与 least sum of square 中得出的估计量相同,但 \(\hat{\sigma ^2} = \frac{\Sigma _{i=1} ^n e_i ^2}{n}\)。注意这是一个有偏的估计量,而 least sum of square 得到的估计量是无偏的。
推断复习
咕了。什么嘛,我推断学得还是可以的嘛(x
Lecture 3
线性回归中的推断
回顾一下,无论是 OLS 方法还是 MLE 方法,我们得到的参数估计 \(b_0\),\(b_1\) 都是相同的:
\[b_1 = \hat{\beta_1} = \frac{\Sigma_i (X_i - \bar{X})(Y_i - \bar{Y})}{\Sigma _i (X_i-\bar{X})^2}\]
\[b_0 = \hat{\beta_0} = \bar{Y} - b_1 \bar{X}\]
通过简单的计算可以知道:
\[E(b_1) = \beta_1,Var(b_1) ={\sigma^2 \over S_{XX}},s^2(b_1) = \frac{s^2}{S_{XX}}\],
其中 \(S_{XX} = \Sigma_{i=1} ^n (X_i - \bar{X})^2\), \(s^2 = \hat{\sigma}^2 = \frac{\Sigma_{i=1}^n e_i^2}{n-2}\)。
而且有 \(Cov(b_1, \bar Y)=0\)。
参数推断
对 \(\beta_1\) 进行推断:null hypothesis 为 \(H_0: \beta_1 =0\),这样设置是因为关心两个变量之间是否存在线性关系。
在假设 \(H_0\) 下可以考虑 test statistic 为 \(T= \frac{b_1 -0}{s(b_1)} \sim t_{n-2}\),这是因为 \(H_0\) 假设下 \(b_1-0 \sim N(0,\frac{\sigma}{\sqrt{Sxx}})\),我们一般用 \(\sigma\) 的无偏估计 \(\hat{\sigma} = \sqrt{\frac{\Sigma_{i=1}^n e_i ^2}{n-2}}\) 来处理。
level of significance 为 \(\alpha\),于是当 observed data \(t_0\) 满足 \(|t_0| > t_{n-2,1-\alpha /2}\) 时 reject \(H_0\)。
如果没有拒绝 \(H_0\),通常的可能有以下三种:
- 发生了 Type II Error,没有成功拒绝掉 \(H_0\) 而事实相反;
- \(X\) 和 \(Y\) 之间确实没有什么线性关系;
- \(X\) 和 \(Y\) 之间有关系,但是非线性。(这句话原来的 typo 是“有线性关系,但是非线性”,绷不住了,中午被 Photon 指出来了,非常感谢他)
对 \(\beta_1\) 做 confidence interval:由于在 \(\beta_1\) 代表斜率的情况下,有 \(\frac{b_1 - \beta_1}{s(b_1)} \sim^{H_0} t_{n-2}\)。
于是 \(P(\frac{|b_1-\beta_1|}{s(b_1)} < t_{n-2,1-\alpha /2}) = 1-\alpha\),\(\beta_1\) 的 100%\((1-\alpha)\) confidence interval 是
\[(b_1 - t_{n-2,1-\alpha /2} s(b_1),b_1 + t_{n-2,1-\alpha /2} s(b_1))\]
类似地可以对 \(\beta_0\) 做推断,有 \(\frac{b_0 -\beta_0}{s(b_0)} \sim t_{n-2}\),因此如果 null hypothesis 为 \(H_0: \beta_0 =0\),rejection region 即为满足条件 $ > t_{n-2,1-/2} $ 的数据。对于偏移的 null hypothesis \(H_0 : \beta_0 =c\),也只要相应地移动 rejection region 即可。
100%\((1-\alpha)\) confidence interval 为 \((b_0 - t_{n-2,1-\alpha /2} s(b_0),b_0 + t_{n-2,1-\alpha /2} s(b_0))\)。
实际上我们一般对 \(\beta_0\) 的推断不感兴趣,因为这个参数未必有意义,依赖于 \(X\) 的取值范围。
以上都是对单个参数进行推断,实际上我们也可以进行 joint inference:
同时推断两个参数 \((\beta_0,\beta_1)\),这时候得到的就是 confidence region,使得 \(P((\beta_0,\beta_1) \in S \subset \mathbb R^2) = 100(1-\alpha) \%\)。实际上因为 \((b_0 , b_1) ^T \sim N((\beta_0,\beta_1)^T , \sigma^2 \Sigma_{2\times 2})\),所以最小的 confidence region 是一个椭圆。
实际上我们也可以考虑做一个矩形的 confidence region,也即对两个参数分别作 confidence interval,confidence coefficient 分别为 \(\sqrt{1-\alpha} \approx 1-\frac{\alpha}{2}\)。因此 confidence region 为:
\[ (b_1 - t_{n-2,1-\alpha /4} s(b_1),b_1 + t_{n-2,1-\alpha /4} s(b_1)) \times (b_0 - t_{n-2,1-\alpha /4} s(b_0),b_0 + t_{n-2,1-\alpha /4} s(b_0))\]
参数推断的角度来说 \(\beta_1\) 的推断远比 \(\beta_0\) 重要,它表征线性关系,而且从预测的角度来说,\(\beta_1\) 的推断如果不够精细,会导致远离 \(\bar X\) 处的 \(X_h\) 对应的估计量误差很大。
Power Function
一个 significance test 的 power 指的是 reject \(H_0\) 时 \(H_1\) 是正确的的概率,也就是 \(1-P(\)Type II Error\()\)。实际上一个推断是好的的情况下需要既不 over-powered 也不 under powered,这和 Type I Error 与 Type II Error 此消彼长的性质有关。
Power function 一般是一个关于参数的函数。以推断 \(\beta_1\) 的过程为例,计算这一推断的 power function。
我们在线性回归参数推断里会用到一种非中心化 t-分布。普通的 t-分布是关于 \(x=0\) 对称的,非中心化 t-分布有一定的偏差。注意并不是整体在坐标轴方向上的移动,其形状也发生了变化。表达式为 \(t(df, \delta ) = \frac{N(0,1) + \delta}{\sqrt{\chi_{df} / df}}\)。
对 \(\beta_1\) 进行推断:null hypothesis 为 \(H_0: \beta_1 =0\),这样设置是因为关心两个变量之间是否存在线性关系。
在假设 \(H_0\) 下可以考虑 test statistic 为 \(T= \frac{b_1 -0}{s(b_1)} \sim t_{n-2}\),然而在 \(H_1\) 下,
\[T=\frac{b_1}{s(b_1)} = \frac{b_1 - \beta_1 + \beta_1}{s(b_1)} = \frac{b_1-\beta_1}{s(b_1)} + \frac{\beta_1 / \sigma(b_1)}{s(b_1)/\sigma(b_1)} = \frac{N(0,1) + \delta}{\sqrt{\chi_{df} / df}} \sim t(n-2,\beta_1/\sigma(b_1))\]
于是 \(Power(\beta_1) = P(Reject H_0 | H_1 holds) = P(|T| > t_{n-2,1-\alpha /2} | \beta_1 \neq 0) = P(T<t_{n-2,\alpha /2}) +1-P(T<t_{n-2,1-\alpha /2})\),其中在 \(\beta_1 \neq 0\) 的条件下,\(T\sim t(n-2,\beta_1 / \sigma(b_1))\)。
BLUE
简单来说,OLS Estimators 是 the best linear unbiased estimator,简称 OLS estimators 是 BLUE。best 的意思是方差最小,这是不难证明的。
BLUE 是非常好的性质,也希望我以后能 go blue(逃
2025.12.02 upd: 这是什么预言家,反正我是 go 过 blue 了(逃
Lecture 4
Prediction & ANOVA,感谢 zzy 救我的生统概论(
Estimation & Prediction
平均响应的推断
有了线性回归模型之后当然是要用来做预测,通过已有数据拟合出一个线性模型,再用来估计未知点的值。对于需要估计的点 \(X_h\),一般来说估计值都是考虑平均响应 (mean response) \(\mu_h = E(Y_h) = \beta_0 +\beta_1 X_h\),把 \(\hat{\mu_h} = b_0 + b_1 X_h\) 作为 \(\mu_h\) 的估计。这是一个 estimator,既然如此就要考虑它的性质,也要先考虑平均响应的置信区间。
\(E(\hat{\mu_h}) = E(b_0) + E(b_1)X_h = \beta_0 + \beta_1 X_h = \mu_h\) ,是 unbiased estimator
\(Var(\hat{\mu_h}) = Var(\bar{Y}+ b_1(X_h - \bar{X})) = \sigma^2 [\frac{1}{n} + \frac{(X_h - \bar{X})^2}{\Sigma (X_i -\bar{X})^2}]\) ,是 minimum variance
\(\hat{\mu_h} = \bar{Y} + (X_h - \bar{X}) b_1\),由于 \(\bar{Y}\) 和 \(b_1\) 都有正态假设,因此 \(\hat{\mu_h}\) 也服从正态分布,\(\hat{\mu_h} \sim N(\mu_h , Var(\hat{\mu_h}))\)。
\(Var(\hat{\mu_h})\) 的估计量是 \(s^2(\hat{\mu_h}) = s^2[\frac 1 n + \frac{(X_h-\bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\),于是有 \(\frac{\hat{\mu_h} - \mu_h}{s(\hat{\mu_h})} \sim t_{n-2}\)。
因此,\(\mu_h\) 的 \(100 \% (1-\alpha)\) confidence interval 是 \((\hat{\mu_h} - t_{n-2, 1-\alpha /2} s(\hat{\mu_h}),\hat{\mu_h} + t_{n-2, 1-\alpha /2} s(\hat{\mu_h}))\)。confidence interval 的长度为 $2t_{n-2, 1-/2} s() = 2t_{n-2, 1-/2} s $,其中 \(s = \sqrt{[\frac{\Sigma_{i=1}^n e_i^2}{n-2}]}\)。因此置信区间的长度是近似于随 \(X_h - \bar{X}\) 递增而递增的。也就是说,\(X_h\) 距离 \(\bar{X}\) 越远,置信区间的长度越大,准确性越难保证。
综上,我们成功找到了这个对于 \(\mu_h\) 的估计的置信区间。
预测值的推断
上述估计的是预测值的平均响应,对于新观测点的值需要改成:\(Y_{h(new)} = \beta_0 + \beta_1 X_h +\varepsilon\) 且有 \(E(\varepsilon) = 0,Var(\varepsilon) = \sigma^2\)。注意这里 \(\varepsilon\) 是随机变量,\(\beta_0,\beta_1\) 是未知值的参数,\(X_h\) 是已知的常数。
对它做估计 \(\hat{Y}_{h(new)} = \hat{\mu_h} = b_0+b_1 X_h\) 仍然是和平均响应相同,考虑这个估计的性质。
\(E(\hat{Y}_{h(new)}) = E(b_0 + b_1 X_h) = \beta_0 + \beta_1 X_h\)
从简单的情形开始,如果 \(\beta_0,\beta_1,\sigma\) 都是已知的参数,则在正态假设下 \(\frac{Y_{h(new)} -E(Y_h)}{\sigma}\sim N(0,1)\)(非正态假设情况下服从未知分布),\(Y_{h(new)}\) 的 confidence interval 是 \((E(Y_h) - z_{1-\alpha /2} \sigma,E(Y_h) + z_{1-\alpha /2} \sigma)\)。
一般情况下,设 \(d_h = Y_{h(new)} - \hat{Y}_{h(new)} = Y_{h(new)} - \hat{\mu_h}\),于是有 \(E(d_h) = 0\)。
计算可知方差 \(Var(d_h) = Var(Y_{h(new)} - \hat{\mu} _h) = Var(Y_{h(new)})+Var(\hat{\mu_h}) = \sigma^2[1+\frac 1 n +\frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\);
standard error 为 \(s^2(d_h) = s^2 [1+\frac 1 n +\frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\);
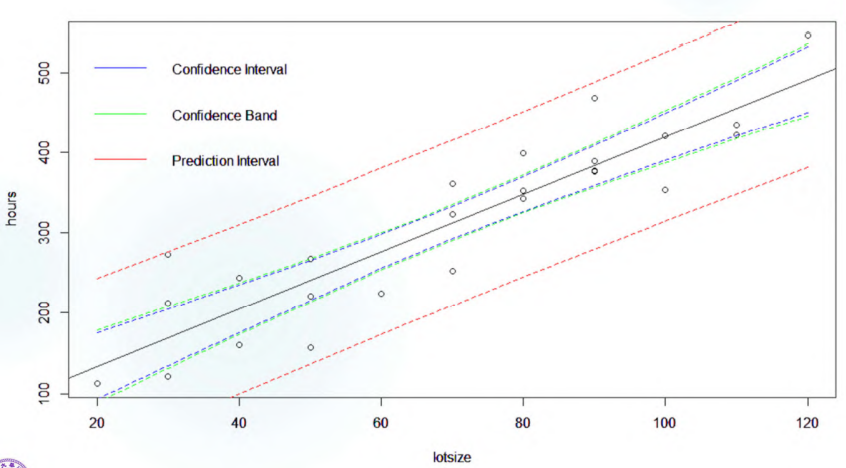
于是有 \(\frac{d_h - E(d_h)}{s(d_h)} = \frac{d_h}{s(d_h)} = \frac{Y_{h(new)} - \hat{\mu}_h}{s(d_h)} \sim t_{n-2}\),\(Y_{h(new)}\) 的置信区间是 \((\hat{\mu}_h - s(d_h) t_{n-2,1-\alpha/2},\hat{\mu}_h + s(d_h) t_{n-2,1-\alpha/2})\),这个区间一般叫做 prediction interval,长度是 \(2 t_{n-2,1-\alpha/2} s(d_h)\),其中 \(s^2(d_h) = s^2 + s^2(\hat{\mu}_h ^2)\),因此预测区间比平均响应的置信区间略宽。
预测值的平均的推断
考虑在新值 \(X_h\) 处的 \(m\) 个观测值的平均值,为 ${Y_h} = m {i=1} ^m Y{h(new) i} = _0 +1 X_h+ 1m {i=1}^m _i $,预测值的平均仍然是 \(\hat{Y_h}=b_0 + b_1 X_h\)。有 \(\varepsilon _i \sim N(0,\sigma^2)\) 为正态假设。于是 \(Var(\bar{Y}_h - \hat{Y_h}) = \sigma^2 [\frac 1m + \frac 1 n + \frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}] \leq Var(d_h)\)。
它的宽度小于 prediction interval,但也大于平均响应的 confidence interval。
Confidence Band for Entire Regression Line
怎么翻译都没那味,就写原文吧。
希望找到一个 confidence band:\(\lbrace (x,y): L(x)<y<U(x), x\in \mathbb R \rbrace\),对于任意点 \(x\) 有 \(P[l(x) < \beta_0 +\beta_1 x <u(x)] = 1-\alpha\)。对于固定的点 \(x\),\(100 \% (1-\alpha)\) 置信区间为 \((\hat{\mu_x} - t_{n-2, 1-\alpha /2} s(\hat{\mu_x}),\hat{\mu_x} + t_{n-2, 1-\alpha /2} s(\hat{\mu_x}))\)。
所以只要取 \(W=max\{(\hat{\mu}_x - \mu_x)/s(\hat{\mu}_x) \}\),即有置信区间为 \((\hat{\mu}_x - W s(\hat{\mu_x}),\hat{\mu}_x + W s(\hat{\mu_x}))\),其中 \(W = \sqrt{2F_{1-\alpha,2,n-2}}\)。实际上 \(W > t_{n-2,1-\alpha /2}\),也就是说 confidence band 处处比 confidence interval 更宽,level of confidence \(\alpha'\) 也更小。
Summary
一个显示 confidence interval of mean response,prediction interval 和 confidence band 宽度关系的图:
Analysis of Variance (ANOVA)
Variance Estimator
先上点概念:
Total Sum of Squares: \(SST= \Sigma(Y_i - \bar{Y})^2\),\(df_{SST} = n-1\)
Sample Variance: \(S_n ^2 = \frac{SST}{n-1}\),是非常熟悉的统计量。
Variation due to Error: \(SSE = \Sigma(Y_i -\hat{Y}_i)^2= \Sigma e_i ^2\), \(df_{SSE} = n-2\)
Mean Square Error: \(MSE = \frac{SSE}{df} = \frac{\Sigma_{i=1} ^n e_i ^2}{n-2}\),可以作为 \(\sigma^2 = Var(\varepsilon)\) 的一个估计。
\(E(MSE) = \sigma^2\)
Variation due to Regression: \(SSR = \Sigma(\hat{Y}_i - \bar{Y})^2 = b_1 ^2 \Sigma (X_i-\bar{X})^2\), \(df_{SSR} = 1\)
Mean Squares of Regression: \(MSR = \frac{SSR}{df} = SSR\)
$E(MSR) = E(SSR) = E(b_1 ^2) ((X_i - {X})^2)= ^2 + _1^2 (X_i - {X})^2 $;
可以计算得到 \(SST=SSE+SSR\),自由度方面也是 \(df_{SST} = df_{SSE}+df_{SSR}\)。
事实上在 Lecture 2 中我们考虑过是选取 sample variance 还是选取 MSE 作为 \(\hat{\sigma}^2\),这里的定义给出了更清晰的答案:\(SSE\) 更加注重原值和模型之间的联系,把 \(\hat{Y_i}\) 作为 \(Y_i\) 的估计值,在 sample variance 中是把 \(\bar{Y}\) 作为 \(Y_i\) 的估计值,前者更好地体现了 \(\varepsilon\) 的场景。
F-检验
我们希望通过以上统计量检验 \(X,Y\) 之间是否存在线性关系。考虑假设 \(H_0: \beta_1 = 0 ; H_1 : \beta_1 \neq 0\)。
在正态假设和 \(H_0\) 成立条件下,取 test statistic 为 \(F= \frac{MSR}{MSE} = \frac{SSR / df_R}{SSE / df_E} = \frac{\chi_{dfR}/df_R}{\chi_{dfE}/df_E} \sim F_{df_R,df_E} = F_{1,n-2}\)。考虑拒绝 \(H_0\) 的情况,我们要求 \(F_0 > F_{1-\alpha,df_R,df_E} = F_{1-\alpha, 1,n-2}\),满足此条件的 \((X,Y)\) 构成 rejection region。或者从 P-value 的角度来看,满足不等式 \(P(F>F_0 | F_{1,n-2}) < \alpha\) 的全体 \((X,Y)\) 落在 rejection region 中。
考虑检验的 power function。在 \(H_1: \beta_1 \neq 0\) 条件下,Power(\(\beta_1\)) = \(P(F> F_{1-\alpha , 1,n-2} | non-central F)\)。
General Linear Test
另一种检验上述假设的方式。考虑假设 \(H_0: \beta_1 = 0 ; H_1 : \beta_1 \neq 0\),我们来比较两种不同的模型:
full model: \(Y_i = \beta_0+\beta_1 X_i +\varepsilon _i\),reduced model: \(Y_i = \beta_0 + \varepsilon_i\),在 \(H_0\) 假设成立时两个模型是等价的。考虑方差统计量:
- \(SSE(F) = SSE\) for full model with \(df_{EF}\),在 simple linear regression 下 \(df_{EF}=n-2\),\(SSE(F) = SSE\)
- \(SSE(R) = SSE\) for reduced model with \(df_{ER}\),在 simple linear regression 下 \(df_{ER}=n-1\),\(SSE(R) = SST\)
在 \(H_0\) 假设下,$F = F_{(df_{ER}-df_{EF}),df_{EF}} $。实际上,在 simple linear regression 下和 F-检验是一致的。但是 general linear test 是一个更广泛的方法,可以用于任何形式的线性检验。
Pearson Correlation r
\(r = \frac{\Sigma (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\Sigma(X_i - \bar{X})^2} \sqrt{\Sigma(Y_i - \bar{Y})^2}}\) 被称为相关系数,反映了一组数据 \((X,Y)\) 之间的线性关系程度。
\(R^2 = \frac{SSR}{SST}\) 被称为决定系数,事实上在 simple linear regression 下有 \(r^2=R^2\),因为 \(r = b_1 \frac{\sigma_X}{\sigma_Y}\)。

Lecture 5
回顾一下简单线性回归的模型假设:\(Y_i = \beta_1 X_i + \beta_0 +\varepsilon _i\)
- \(\varepsilon _1, \varepsilon _2 ,..., \varepsilon_n\) 相互独立
- \(\varepsilon_i\) 服从正态分布
- \(\mathbb E(\varepsilon _i) = 0\),\(Var(\varepsilon_i) = \sigma^2\)
可以总结成 LINE: linearity, independence, normality, equal variance
Diagnostics of X
诊断的方式粗暴一点来说就是肉眼诊断,用一些可视化工具(主要是画图)和其他方式来检验模型的假设是否符合。如果违反了模型假设,结果很有可能不可靠。此时需要用一些弥补的方式来处理。
Why diagnose——Distribution and Confounding
诊断过程需要关注的是 \(X\) 而非 \(Y\),因为 \(Y\) 之间是独立异分布的。\(Y_i \sim N(\beta_0 +\beta_1 X_i , \sigma^2)\)。
\(X\) 完全是常数,所谓的 \(X\) 的分布指的仅仅是 \(X_1,X_2,...,X_n\) 在数轴上的排布,不是概率分布。但 \(X_i\) 的分布会影响到模型的效果,直观上举个例子来说,\(X_i\) 的位置至少会影响到 \(Var(b_1) = \frac{1}{\Sigma_i (X_i - \bar X)^2} \sigma^2\) 也就是 \(b_1\) 的分散程度,这是会影响到推断显著性的因素,所以即使是常数也还是要对 \(X\) 进行一些诊断。
我们一般希望 \(X\) 是类似于正态的分布,这样的数据比较有代表性。可以使用 qq-plot 进行检查。
除此之外诊断 \(X\) 的另一意义在于 \(X\) 本身可能也是和其他因素有混杂的。举个例子来说,如果高温既会导致冰激凌销量增加又会导致鲨鱼攻击人的次数增加,很可能会发现冰激凌销量和鲨鱼攻击行为次数之间有线性的关系,事实上这就是一个没有选对合适的 explanatory variable \(X\) 却得到了看似合理的模型的例子,但这样的结论是有问题的,\(X\) 本身和气温这一因素混杂。
此时如果分别对冰激凌销量-气温和鲨鱼攻击行为-气温作一个 sequence plot,会发现二者都分别和气温有关系,那就有必要把气温作为一个 explanatory variable 加入模型的考虑,这是一种针对 confounding 的诊断方法。
四参数
有一些可以关心的量(甚至不能说是统计量,毕竟 \(X\) 也不是随机变量),除了 range 之外实际上就是一阶到四阶矩:
- sample mean 展现了 \(X\) 的主要位置
- standard deviation 展现了数据的分散程度
- 偏度 skewness \(g_1 = \frac{m_3}{m_2 ^\frac 3 2} = \frac{\frac 1 n \Sigma_{i=1}^n (x_i - \bar x)^3}{(\frac 1 n \Sigma_{i=1}^n (x_i -\bar x)^2)^\frac 3 2}\) 展现了数据的对称性
- 峰度 kurtosis \(g_2 = \frac{m_4}{m_2 ^2} -3 = \frac{\frac 1 n \Sigma_{i=1}^n (x_i - \bar x )^4}{(\frac 1 n \Sigma_{i=1} ^n (x_i -\bar x)^2)^2} - 3\) 展现了数据相对于正态分布的尾迹
- range 展现了 \(X\) 的分布范围
其中值得关注的是偏度和峰度两个统计量,因为之前没有提过。想起来一个乐子,Pearson
在《Lady Tasting
Tea》里曾经认为一个分布只要有一阶到四阶矩的参数就可以完全确定,但实际上
Poisson 分布的四个参数都是 \(\lambda\),是不行的。
关于偏度:
- \(g_1 <0\) 时称为 negatively skewed,左尾比较长,所以也会称为 skewed left
- \(g_1 >0\) 时称为 positively skewed,右尾比较长,所以也会称为 skewed right
由图可见偏度是能够体现数据的对称程度的。实际上对称程度是相对正态分布而言的。
一般来说对于一个左偏的分布,会有 mean < median < mode(众数),如果右偏则会是 mode < median < mean。当然 mean 和 median 的顺序不一定准确,以及对于完全对称的分布会有三者相等。
注意如果分布有多个峰值,此时 skewness 不一定还适用。
关于峰度:
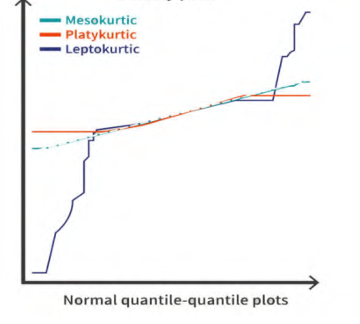
- \(g_2>0\) 时称为 leptokurtic,尖峰态下双尾较长。
- \(g_2 <0\) 时称为 platykurtic,低峰态下双尾较短。
注意峰度的所谓尖峰态低峰态和尾部数据性质也都是相对正态分布而言的。正态分布的峰度就是 \(3\),因此峰度的公式里有一个减去 \(3\) 的操作,作为和正态分布的比对。
有的时候会把不减去 \(3\) 的称为 kurtosis,减去 \(3\) 则称为 excess kurtosis,使用的时候要注意。
实际上峰度带来的度量信息包括峰和尾两部分,单独出现尖峰的条件不能作为判断 \(g_2\) 正负性的依据,只是表征了 \(\bar X\) 附近的情况,和尾部情况综合起来看才可以;峰度的正负性和方差的大小无关。
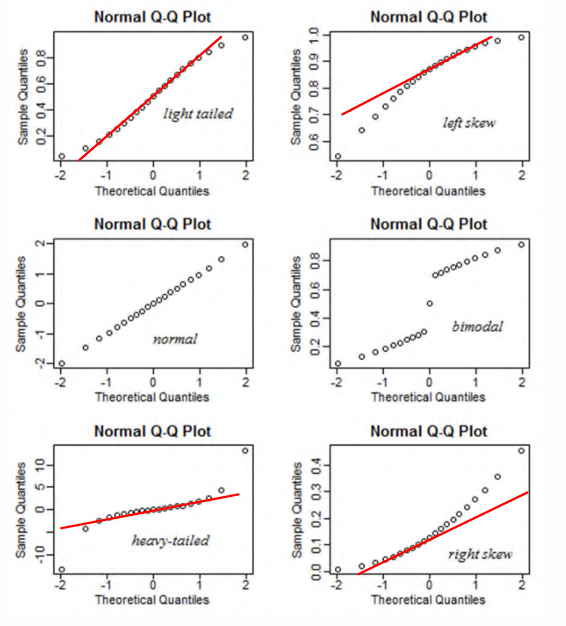
尾部的情况可以通过 Q-Q plot 查看:
诊断 assumptions
最常用的 assumption 诊断方法是使用残差图进行诊断,一元线性回归中我们可以直接使用 \(e_i \sim X\) 图,也可以使用 \(e_i \sim \hat Y\) 图进行诊断,二者本质上只相差横轴的尺度和位置。在多元线性回归中就直接使用 \(e_i \sim \hat Y\) 图进行诊断。
除此之外也有很多理论检验的方法,虽然听起来更 concrete,但其实实际应用中还是肉眼检查最有效。
模型诊断可能发现的一些问题:
- \(Y\) 和 \(X\) 之间没有线性关系但是硬拟合了一个
- \(\sigma ^2\) 不能视作常数,也即异方差
- \(\varepsilon _i\) 不服从正态分布
- \(\varepsilon _i\) 之间彼此不独立
- 模型可以拟合,但数据中有 outlier
以下给出一些发现问题的方法:
非线性关系
简而言之,\(Y\) 和 \(X\) 之间可能并不是一个线性关系,但是我们采用了线性模型进行拟合。
找出问题的手段是使用 \(e_i \sim
X_i\) 图诊断 \(Y\) 和 \(X\) 的线性关系是否过拟合。具体来说,给
\(e_i \sim X_i\) 再做一个拟合图线
scatter.smooth,观察和 \(h=0\) 是否偏离较大。虽然通过 \(Y \sim X\) 也可以看出来,但是 \(e_i \sim X\) 图更加明显。
即使线性关系是显著的(R 中得到 \(R^2\) 较大、斜率 \(\beta_1\) 显著),也不说明线性模型是最好的拟合模型。
异方差问题
实际上的残差并不符合方差相等的假设,则称为异方差问题。即使发生这样的情况也未必会影响到 \(\beta_1,\beta_0\) 的估计值,因为计算过程和这一假设实际上是无关的。但是,异方差问题会导致 \(b_0,b_1\) 不再是使得方差最小的估计,失去了 BLUE 性质,但仍然是无偏的估计。问题会反映在关于 \(\beta_1,\beta_0\) 的推断中,导致推断或者置信区间不是效率最高的。
举个例子,比如说 \(Y_i = 30 +100X_i + 10X_i \varepsilon_i\),实际上是有 \(\varepsilon_i \sim N(0,10X_i \sigma^2)\),方差并不相同。
画图检查最典型的异方差情况是画出 \(e_i \sim X\) 图后发现 \(X\) 越大,\(e_i\) 越分散,呈现出一个扇形的分布形态。
模型的诊断也可以使用一些理论方法,异方差检验中常用的几种检验如下所示:
Bartlett 方法,本质上是 likelihood ratio test,但非常依赖残差的正态假设。也即,如果检验结果是拒绝原假设,未必是真的发生了异方差现象,也可能是因为残差不服从正态分布造成了干扰。
Levene & modified Levene (B.F.) 方法,非常常见。
对于可能影响方差导致异方差的因素 \(Z\),将 \(e_i ^2\) 相对于 \(Z\) 再做一次线性回归,得到的 SSR 记为 \(SSR^*\)。
此时 \(LM = \frac{SSR^*/2}{(SSE/n)^2} \sim \chi_1 ^2\) 再进行检验。
正态性假设
\(\varepsilon _i\) 并不服从正态分布,这可以通过 QQ-plot 观察是否有 \(\varepsilon_{(i)} = \mu + \sigma Z_i\),或者直接画 histogram 检查是否有正态的形状。
理论方法之中 Shapiro-Wilk 方法是最佳的,有最大的 power,但是对于样本量是敏感的。也就是说,如果检验结果是 \(\varepsilon_i\) 不服从正态分布,也可能是因为样本量太大导致了错误判断。
注意正态性检验是完全可以把 \(\{\varepsilon _i \}\) 作为一组数据放在一起观察整体的分布的,但是对 \(\{Y_i \}\) 不可以这样做,它们彼此之间服从的是不同的条件分布。
相关性
\(\varepsilon_i\) 之间可能并不独立,有可能都受到 \(t_i\) 的影响,等等。如果有类似可能考虑的因素可以对其做 sequence plot。
理论方法中最常用的是 Durbin-Watson 方法。
Outlier
模型的数据里有 outlier,不同性质的 outlier 对回归线的影响不尽相同,具体的在 Lecture 6 中再细说。简单来说就是,outlier 的 \(X_i\) 越接近 \(\bar{X}\),对于回归线的斜率影响越小,但如果距离 \(\bar{X}\) 比较远,则会产生比较强的杠杆效应。
即使模型中存在 outlier,参数的估计也可以是比较准确的。做 \(e_i \sim X\) 图可以查看是否存在 outlier,也可以使用 \(Y_i \sim X_i\) 的图来观察是否有距离回归线很远的点,这是最明显的一类 outlier。然后可以尝试剔除这样的点再重新做回归,检查各系数。
关于 \(R^2\)
如果在某一线性模型中得到 \(R^2 = 0.69\),能否说明这一线性模型是显著的?
- 事实上可以。\(R^2 = 0.69\) 已经是相对大的数值了,说明模型对于方差的解释能力是相对好的;另一方面考虑 \(r = \sqrt{R^2} > 0.8\),相关系数其实是比较大的,可以认为这一模型是合适的。
- 但是,这并不能说明线性模型是这一问题下最好的模型。\(R^2\) 想要多大就可以多大,例如给模型加入新的多项式型变量,总能更多地解释一些方差,不能单纯地追求 \(R^2\) 的大小。
- 另外,如果在不同的模型比较中对 \(\{Y_i \}\) 做了变换,比如进行了标准化或者 Box-Cox transform,此时是不能和原始的模型再进行 \(R^2\) 的比较的,只能检查单个 \(R^2\) 的值能否接受。这是因为 \(SST\) 已经随着 \(\{Y_i \}\) 的变化而变化了,模型的方差解释能力 \(\frac{SSR}{SST}\) 无法比较。
Lecture 6
Built-in Diagnostic Plots in R
R 内置的四个诊断图是 \(e_i \sim \hat Y\),Q-Q plot,\(\sqrt{|\text{Standardized Residuals}|} \sim \hat Y\),Cook's distance 图。前两个都比较简单,一个是万能的残差图,另一个是残差的正态性检验,主要说一下后两个图。
Scale-Location Plot
\(\sqrt{|\text{Standardized Residuals}|} \sim \hat Y\) 作图体现了 residuals 随拟合值的分布情况,主要用来检验异方差。实际上在上一讲里面是直接用 \(e_i \sim X\) 来检验异方差的,这里用了标准化的残差开方,有一些考虑:
关注 magnitude 所以需要一个正值,选择了先取绝对值
取绝对值之后的数据往往人为造成了右偏,开方可以缓解一些
standardize 之后绝大多数 \(e_i\) 都收入了 \([-2,2]\) 这一范围内(正态分布的主要区间),更清晰,有可比性
虽然理论上的 \(\varepsilon_i\) 是独立分布的,但是残差之间是有约束关系的,\(Var(e_i) = (1-h_{ii})\sigma^2\),也就是说 \(e_i\) 的变动范围本身就和其在 \(x\) 轴上的位置(也即 \(X_i\) 的大小)相关。较大的 \(X_i\) 会对应 \(e_i\) 的更大方差,导致可能会看起来像异方差。
标准化并开方能够一定程度缓解这样的问题。
如果此图上的残差点分布看起来比较随机,拟合线也相对平行于 \(x\) 轴,基本可以认为是异方差。
Cook's Distance
图中被标出数字的点/靠近右上角和右下角/红线之外的点需要重视一下,是 high leverage point 或者 outlier,可以进一步检验。
Residuals & Leverage
Leverage
定义每一点的杠杆值为 \(h_{ii} = \frac{\partial \hat Y_i}{\partial Y_i} \in [0,1]\),表征了某一个 \(X_i\) 对应的 \(Y_i\) 变动一个单位时,会导致回归线上的响应值变动的大小,也就是说,这一点的变化对于整个回归模型的影响。
事实上,\(X_i\) 对应的点的 leverage 是 \(h_{ii} = \frac 1 n + \frac{(X_i - \bar X)^2}{\Sigma_j (X_i - \bar X)^2}\),\(h_{ii}\) 越大会导致 \(Var(e_i) = (1- h_{ii})\sigma^2\) 越小,因此 \(e_i\) 的变动范围变小,\(\hat Y_i\) 能够变动的范围也较小,会导致回归线受较大的影响;从 leverage 的表达式可以看出来,\(|X_i -\bar X|\) 越大会导致杠杆值越大,也就是说远离中心的点对回归线造成的影响较大。
我们对 extreme values 做一些分类:
Outlier: 离群值是对于其 \(Y\) 值而言的,\(Y_i\) 的实际取值远离通常该有的范围,则这一点会被认为是 outlier。
High Leverage Point: 高杠杆值点是对于其 \(X_i\) 的取值而言的,由上述分析可以得到 \(h_{ii}\) 较大的主要条件。
Influential Point: 强影响力点指的是移除此点后,回归线会发生较大的变化的点。
如果一个点既是 outlier 又是 high leverage point,那它一定是 influential point,直觉上来看是因为它的 \(X\) 和 \(Y\) 都具有一定的特征,会对回归线造成较大的影响。
如果 \(h_{ii} > 2p/n\) 一般就称为高杠杆值点。
Studentized Residual
一个 influential point 造成回归线的巨大改变无法在残差图上体现出来,因此我们希望有一种手段能够体现出它和其他正常点的巨大差异。一个自然的想法是先移除它再做回归线,然后在这一模型上体现残差,即为 studentized residual。
这么说还是太抽象了,放个图好了:
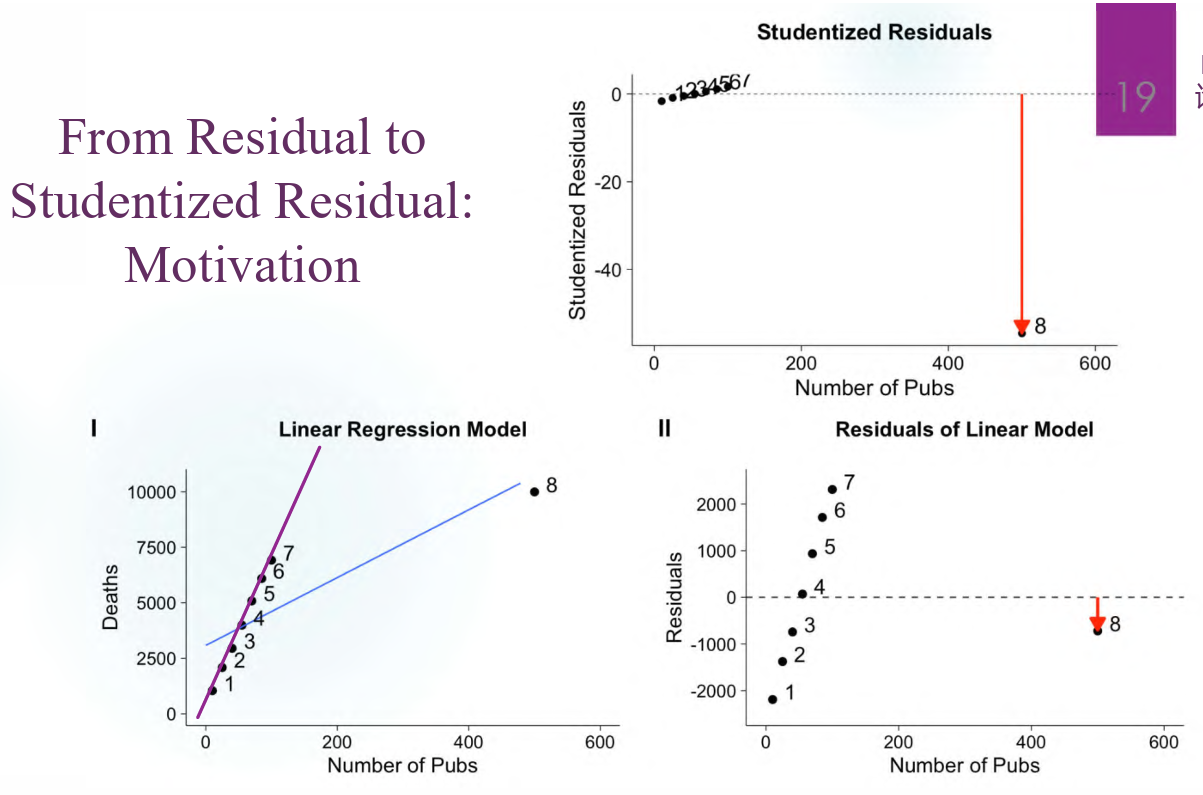
具体来说,studentized residual 和 standardized residual 有一些差别:
standardized residual: \(\frac{e_i}{s(e_i)}\),由于 \(Var(e_i) = (1-h_{ii})\sigma^2\),则 \(s^2 (e_i) = (1-h_{ii})MSE\),代入即可。
deleted residual: \(d_i = Y_i - \hat Y_{i(-i)}\),其中 \(\hat Y_{i(-i)}\) 是 \(X_i\) 在去除这一点的模型中所对应的响应。
studentized residual: \(\frac{d_i}{s(d_i)}\),同理有 \(s^2(d_i) = (1-h_{ii})MSE_i\),\(MSE_i\) 是去除第 \(i\) 点的模型对应的 MSE。
事实上 \(e_i^* = \frac{d_i}{s(d_i)} = \frac{e_i}{\sqrt{MSE(1-h_{ii})}}\) 是 internal studentized residual,当 \(|e_i ^*| >2\) 时认为是一个 outlier。
studentized deleted residual 如下所示:

Cook's Distance
考虑 \(D_i = \frac{\Sigma_j (\hat Y_j - \hat Y_{j(-i)})^2}{ps^2}= \frac{e_i^2}{p\cdot MSE} \frac{h_{ii}}{(1-h_{ii})^2}\),其中 \(\hat Y_{j(-i)}\) 指的是 \(X_j\) 在去除第 \(i\) 点的模型中对应的平均响应值。第 \(i\) 点的 Cook's distance \(D_i\) 表征的是第 \(i\) 点的值对全体预测值(也就是回归线)的影响力。\(D_i\) 越大越说明这是个 high influential point,一般吧 threshold 作为 \(0.5\) 或者 \(\frac 4 n\)。
Lack of fit test
怀疑某个模型并不符合线性,且其某一 \(X_i\) 点处有多个对应的 \(Y\),也即这一点处存在 replicates 或者说 repeated observation 的时候,可以进行失拟检验。具体来说,可以进一步细分 SSE 为 sum of pure error 和 sum of lack of fit error,前者由数据的随机性导致,后者由线性模型的失拟性造成。
事实上也是 general linear test 的一种,这里的 full model 就是 cell mean model \(Y_{ij} = \mu_i + \varepsilon_{ij}\),reduced model 是线性模型 \(Y_{ij}=\beta_0 +\beta_1 X_i + \varepsilon_{ij}\)。也就是说,实际上的 \(H_0: \mu_i = \beta_0 + \beta_1 X_i\),拒绝 \(H_0\) 时说明 reduced model 失拟。
对 SSE 进行进一步的拆分,将其改变为 \(SSE = SSPE +SSLF\),具体表达式和自由度如下所示:
\[\Sigma_{i=1} ^c \Sigma_{j=1}^{n_i}(Y_{ij} - \hat Y_{ij})^2 = \Sigma_{i=1} ^c \Sigma_{j=1}^{n_i}(Y_{ij} - \bar Y_{i.})^2+ \Sigma_{i=1} ^c \Sigma_{j=1}^{n_i}(\bar Y_{i.} - \hat Y_{ij})^2\]
\[SSE = SSPE + SSLF\]
\[(n-2) = (n-c)+(c-2)\]
因此,对应地有 \(E(MSPE) = \sigma^2,E(MSLF) = \sigma^2 + \frac{\Sigma_i n_i (\mu_i - (\beta_0 + \beta_1 X_i))^2}{c-2}\),test statistic 是 \(F^* = \frac{MSLF}{MSPE} \sim ^{H_0} F(n-c,c-2)\)。
这也就说明了为什么失拟检验只有在存在 replicates 的时候才能做,因为这时才会有 \(n > c\),使得模型不至于退化。
Remedy Methods
补救非线性
通过 \(e_i \sim X\) 观察到模型并不是完全线性的时候,如果不想再改变 assumptions,可以转而选择非线性的模型。
R 中可以调用函数 nls。
补救异方差
可以使用 weighted analysis,具体参见 Lecture 12 的内容。
补救非正态
如果残差体现出非正态分布的性质,可以对 \(Y\)
做变换继续使用线性模型,也可以使用其他的模型来允许残差不同分布。在 R
中可以调用函数 glm。
Transformation
有以下任一需求的时候都可以考虑对 \(Y_i\) 做变换:
- 稳定方差:观察到 \(\varepsilon_i\) 似乎是异方差的
- 提高正态性
- 简化模型,提高解释性
最普遍的方法是 Box-Cox Transformation,取 \(Y^* = (Y^\lambda-1)/\lambda\),首要任务是找到最合适的 \(\lambda\) 做变换。事实上所谓的“最合适”包含两层意义,其一是希望模型拟合程度较高,其二是希望 \(\lambda\) 使得 \(Y^*\) 的形式尽量简洁明了,解释性强,也就是取所谓的 convenient lambda。例如取 \(\lambda=0\) 时有 \(Y^* = \log Y\),取 \(\lambda\) 为整数时即为多项式回归,等等。
另外不同的 \(\lambda\) 值会对数据的右偏有不同程度的改善,右尾压缩最明显的是开根和取对数;也可以取负值来压缩左尾。
在实际使用中往往是直接对 \(\lambda\) 取一个 sequence,找到近似取到 maximum likelihood 或者使得 SSE 最小的 \(\lambda\) 的一个置信区间,再在其中寻找合适的 convenient lambda。
一些典型的数据分布和变换方法:

Miscellaneous Topics
一些杂谈,关于 simple linear regression 的最后内容。
Regression Through the Origin
非常坏回归,爱来自自由度(
强迫过原点回归的时候斜率的估计是 \(\hat \beta_1 = \frac{\Sigma X_iY_i}{\Sigma X_i^2}\),这会导致一些很严重的后果:
- 残差的和 \(\Sigma e_i \neq 0\),这导致 \((Y_i - \bar Y)^2 = (Y_i - \hat Y_i)^2 + (\hat Y_i - \bar Y)^2 + 2(Y_i - \hat Y_i)(\hat Y_i - \bar Y)\) 的交互项无法消去,于是也不能再对 SST 做分解成为 SSE 和 SSR 之和。
- SSE 此时的自由度是 \(n-1\),SST 的自由度也不再是 SSE 和 SSR 的自由度之和。
Inverse Predictions
对 \(Y \sim X\) 做回归得到 \(y = b_0 + b_1 x\) 和对 \(X \sim Y\) 做回归得到 \(x = a_0 + a_1 y\) 中,实际上在绝大多数情况下都有 \(a_1 b_1 \neq 1\)。也就是说,两种回归的结果不能简单地用线性求反函数得到,这听起来有点反直觉但确实是合理的,做 \(Y \sim X\) 回归的目标是取得关于 \(Y\) 的最小残差平方和,做 \(X\sim Y\) 回归的目标是取得关于 \(X\) 的最小残差平方和,目标不一致得到的结果自然不同。
用理论来解释的话,取相关系数 \(r = \frac{\sum (X_i - \bar X)(Y_i - \bar Y)}{\sqrt{\sum (X_i - \bar X)^2} \sqrt{\sum (Y_i - \bar Y)^2}}\),记 \(S_Y = \sqrt{\sum (Y_i - \bar Y)^2},S_X = \sqrt{\sum (X_i - \bar X)^2}\),于是有:
\(b_1 = r \frac{S_Y}{S_X},a_1 = r \frac{S_X}{S_Y}\),因此 \(b_1a_1 = r^2\)。两条回归线之间的夹角是 \(\tan \theta = \frac{1-r^2}{r(\frac{S_X}{S_Y} + \frac{S_Y}{S_X})}\)。
如果对于某个响应值 \(Y_i\) 需要反向预测输入变量 \(X_i\),应该选择 \(\hat X_h = \frac{Y_h - b_0}{b_1}\) 而不是反过来做 \(X\) 关于 \(Y\) 的回归。
Limitations of \(R^2\)
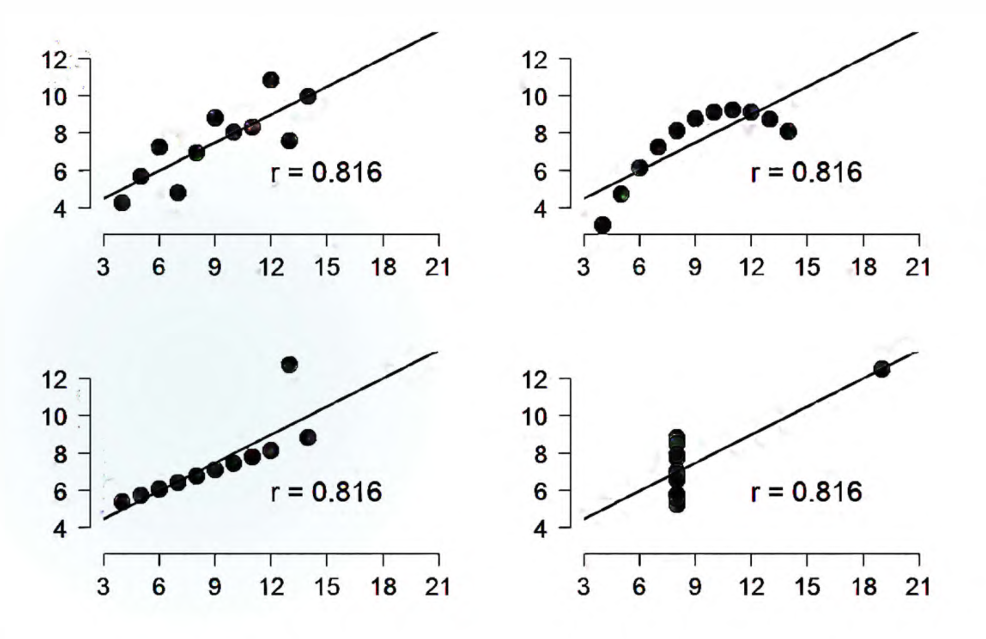
使用 \(R^2\) 作为判断依据的时候要注意以下问题:
\(R^2\) 不能作为拟合程度的度量。\(R^2 = \frac{b_1 ^2 \sum (X_i - \bar X)^2}{\sum (Y_i - \bar Y)^2}\) 的形式显示了,实际上如果把 \(X\) 的取值变得足够分散,\(R^2\) 的取值想要多大就能有多大。
不同的散点分布情况可以得到几乎相同的 \(R^2\),一定要画图检查线性模型是不是最合理的。
不能对于不同的模型比较 \(R^2\),归根结底 \(R^2\) 反映的是模型对于 SST 的解释能力,SST 一旦改变就不能交叉对比。因此上述 transformation 中对于系数 \(\lambda\) 的比选标准是 maximum likelihood。
\(R^2\) 不能显示 \(X\) 和 \(Y\) 之间的因果关系,因为 \(Y\sim X\) 和 \(X \sim Y\) 这两种回归得到的 \(R^2\) 是相等的。
Lecture 7
从一元线性回归过渡到多元回归的部分,介绍回归方程的矩阵表达。
矩阵表达
把 \(n\) 个回归方程的形式改成:
\[\begin{bmatrix}Y_1 \\ Y_2 \\ ... \\ Y_n \end{bmatrix} = \begin{bmatrix}1 & X_{1,1} & X_{2,1} &... & X_{p-1,1} \\ 1 & X_{1,2} & X_{2,2} & ... & X_{p-1,2} \\ ... & ... & ... &... & ... \\ 1 & X_{1,n} & X_{2,n} & ... & X_{p-1,n} \end{bmatrix} \begin{bmatrix}\beta_0 \\ \beta_1 \\ ... \\ \beta_{p-1} \end{bmatrix} + \begin{bmatrix}\varepsilon_1 \\ \varepsilon_2 \\ ... \\ \varepsilon_n \end{bmatrix}\]
\[Y = X \beta + \varepsilon\]
假设 \(\varepsilon \sim N_n(0, \sigma^2 I_{n \times n})\),则有 \(Y \sim N_n(X \beta , \sigma^2 I_{n \times n})\),以下考虑参数矩阵 \(\beta\) 的估计:
\[b = \hat \beta = (X^TX)^{-1} X^T Y \sim N_p(\beta , (X^TX)^{-1} \sigma^2)\]
和 simple linear regression 相同,\(b\) 也有 BLUE 的性质。
因此有 \(Y\) 的平均响应为 \(\hat Y = X \hat \beta = X(X^TX)^{-1} X^TY\),其中记 \(H = X(X^TX)^{-1} X^T\),这就是著名的 hat matrix,围绕它有很多性质,后面再说;由于残差 \(e = Y - \hat Y = (I - X(X^TX)^{-1} X^T)Y\),因此 simple linear regression 中对于 \(e\) 的限制在此处相应地修改为 \(e^T \hat Y = Y^T(I - X(X^TX)^{-1} X^T) (X(X^TX)^{-1} X^T)Y = 0\)。
相应地,\(\sigma\) 的估计量可以改成 \(s^2 = \frac{e^Te}{n-p} = \frac{Y^T(I-H)Y}{n-p}\),这就是 MSE,是 \(\sigma^2\) 的无偏估计;又因为 \(Var(b) = (X^TX)^{-1} \sigma^2\),因此有 \(\hat Var(b) = (X^TX)^{-1} \hat \sigma^2 = s^2 (X^TX)^{-1}\) 是 \(Var(b)\) 的估计。
ANOVA 中的方差和自由度拆分在这里仍然适用:
\[SST = (Y - \bar Y \mathbb 1_n)^T (Y - \bar Y \mathbb 1_n), \quad df = n-1\]
\[SSM = (\hat Y - \bar Y \mathbb 1_n)^T(\hat Y - \bar Y \mathbb 1_n), \quad df = p-1\]
\[SSE = (Y - \hat Y)^T(Y- \hat Y), \quad df=n-p\]
\(F-\)test 的检验统计量是 \(F^* = \frac{MSM}{MSE} \sim^{H_0} F_{p-1,n-p}\),其中假设是 \(H_0 :\beta_1 = \beta_2 = ... =\beta_{p-1}=0\);决定系数 \(R^2 = \frac{SSM}{SST}\) 仍然保持不变,显示了线性模型解释方差的能力;adjusted \(R^2\) 定义为 \(1- \frac{MSE}{MST} = 1- \frac{n-1}{n-p} \frac{SSE}{SST}\),相对于 \(R^2\) 的优势在于,\(R^2\) 在有任意的变量进入模型时都会增大,但如果新变量的显著性不足会导致 adjusted \(R^2\) 下降,是一个更有力的参数。
Hat Matrix
Hat Matrix 有丰富的性质,在这里列举一些和统计关联比较大的。
\[Cov(e) = Cov((I-H)Y) = (I-H)^T \sigma^2 (I-H) = \sigma^2 (I-H)\]
\[Cov(e_i , e_j) = -\sigma^2 h_{ij}\]
\[Var(e_i) = \sigma^2 (1-h_{ii})\]
其中 \(h_{ij}\) 是矩阵 \(I -H\) 的分量。
事实上,第 \(i\) 点的杠杆值就是 \(h_{ii}\)。可以通过 \(H = H^2\) 这一性质简单地证明出 \(h_{ii} \leq 1\),这也和杠杆值的定义是符合的。
Multiple Linear Regression
关于多元回归的系数 \(\beta_1,\beta_2,...,\beta_{p-1}\)(也称为偏回归系数),我们仍然可以按照 SLR 时的方式解释它们:\(\beta_i\) 是在 \(X_1,X_2,...,X_{i-1},X_{i+1},...,X_{p-1}\) 不变时,\(X_i\) 变化一个单位导致 \(E(Y)\) 的变化量。
实际上这就引出了多元回归的一个巨大隐患:并不是所有的变量都完全不相关,一旦 \(X_1,X_2\) 之间有相关性存在,改变 \(X_1\) 的时候很难保证 \(X_2\) 不变,多元回归的系数解释性因此变差。
虽然理论上确实可能存在完全不相关的变量,但是对应的数据也很难不相关。
\(Var(e_i) = \sigma^2 (1-h_{ii})\),因此在线性回归中,位于中间(靠近 \(\bar X\))的 \(X\) 拟合能力较弱(杠杆值低,对回归线的影响较弱)但是预测能力较好(\(Var(e_i)\) 较小,\(\hat Y\) 能够变动的范围小)。相反地,位于两端的 \(X\) 拟合能力较强但是预测能力较弱。
事实上我们是不能轻易预测已有数据范围之外的 \(x\) 的响应的,理由如上所述,此时的预测能力很弱。
Lecture 8
Explanatory Data Analysis——Transformation
Why look at Y
一般来说 \(Y\) 的分布我们是不用太在意的,毕竟不是同分布,但其实考虑到做变换的话还是要稍微看一下它的分布。
如果分布是高度有偏的,做变换把长尾的部分往中央收一收可以得到的效果有:
减小 SST,修正模型的显著性;
把拖尾方向可能的 outlier 向内收,有可能可以变成正常的数据来使用;另一侧原来数据比较集中,做变换如果可以将分布拉长的话便于观察其中的一些特征;
实际上 outlier 并不能随意的扔掉,做变换的想法是能够保留就尽量保留。有些时候很多现象就隐藏在出现了 outlier 这件事情上面,比如臭氧层空洞没有被尽早发现就是因为相关的数据被当成 outlier 扔掉了。
方差对于 skewed data 和 outlier 都比较敏感;
对于 skewed data,均值并不是中心位置很好的显示。
但通常来说做变换之前都需要三思:
- 做变换后可解释性会有问题,比如 Box-Cox Transformation 中奇怪的 \(\lambda\) 取值会导致可解释性变差,实验数据有的时候需要保留单位,做变换之后会失去意义;
- 会导致 \(H_0\) 改变;
- 不一定能够改进正态性,做变换未必有好的效果;
- 做了变换得到结果之后,变回原始数据很可能破坏无偏性;
- 破坏了残差的分布。
有一些平替方案:GLM, resampling methods, non-parametric methods
另外我们一般不会对 \(X\) 做变换,除非做变换之后和 \(Y\) 有非常明确的关系,另一个原因是做变换可能会导致共线性。
Why log Transformation
对 right-skewed data 做 log transformation 的好处是显著多于其他类型的变换的:
- \(\log Y_1 - \log Y_2 = \log (1+ \frac{Y_1 - Y_2}{Y_2}) \approx \frac{Y_1 - Y_2}{Y_2}\),可以把绝对误差变为相对误差来讨论;
- \(\log Y\) 可以让数据的分布更对称,出于计算的考虑
- 如果 \(Y\) 全部都是正数,但 \(Y = X \beta + \varepsilon \sim N(X \beta, \sigma^2 I)\),一个多元正态分布的数据全部是正数的概率非常小,假设不合理。
但是最大的问题就是可解释性。对于参数 \(\beta\) 的解释是在 \(X\) 增长一个单位时 \(Y\) 的平均响应的对应变化,在这里我们选择的是报告平均响应变化的百分比,也即 \(\frac{e^{(X+1)b} - e^{Xb}}{e^{Xb}} = e^b \times 100 \%\),作为一个补救措施。
MLR vs SLR
相比于 simple linear regression,MLR 的变量增多了之后需要考虑的问题也增加了,复杂度也变大了。
变量选择
破事很多:
- 单独一个 \(X_i\) 在模型里不显著也不能直接扔掉,它可能是 suppressor variable,会让别的变量显著
- 多个变量的模型显著不能推出单个变量显著
- 单变量模型中,变量显著性 \(t\) 检验和模型显著性 \(F\) 检验的 p-value 相等,因为 \(F_{1,n} = t_n ^2\)
- 其余变量是否需要进入模型,可以先考虑残差对于其余各个变量的回归显著性,先测试最显著的变量进入模型
有的时候我们认为模型里变量越多越好,有的时候越少越好,这取决于做回归的目的:
- 回归模型是为了预测:变量越多或者说 adjusted \(R^2\) 越大,解释的方差越多,预测水平越好
- 回归模型是为了解释:变量越少,explanatory variable 和 response 之间的关系越明确,解释性越好
总之,会随着模型中进入的变量而改变的参数有:
- 回归系数(\(\hat \beta_i\))
- standard error
- 模型显著性
诡异的现象
有的时候会遇到 Significance & low \(R^2\) 同时出现的情况,也就是某个变量看起来是显著的,但是 \(R^2\) 很低,解释方差的能力并不好。这是正常的现象。
回到 \(R^2\) 的定义和 F 检验的本质可以发现,\(R^2 = \frac{SSR}{SST}, F^* = \frac{MSR}{MSE} = \frac{R^2}{1-R^2} \frac{n-p}{p-1}\),如果 \(n\) 非常大,即使 \(R^2\) 很小也和 \(F^*\) 很大之间并不矛盾。
\(R^2\) 的分母 \(SST\) 实际上表征了数据的分散程度,数据非常分散的时候是可能导致 \(R^2\) 减小的。但是数据分散和存在线性并不矛盾,图中的两个线性关系当然都显著,但是 \(R^2\) 有巨大的差距。
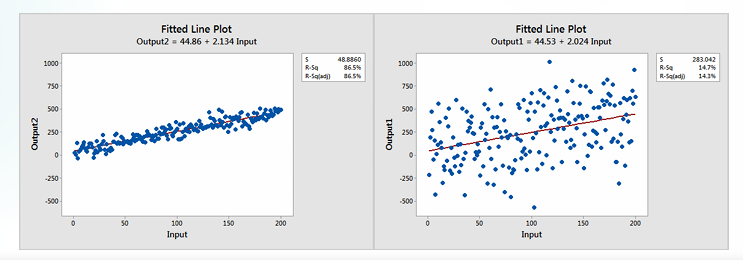
Inference
多重线性回归的推断里面也有一个著名定理:\(Y \sim N_n(X \beta , \sigma^2 I)\),于是有 \(b \sim N_p(\beta , \sigma^2 (X^TX)^{-1})\),以及:
- \(\frac{e^Te}{\sigma^2} = \frac{SSE}{\sigma^2} \sim \chi^2_{n-p}\)
- \(b\) 和 \(SSE\) 相互独立
由此得到很多推断方法。
关于 \(b_k\) 的推断和 CI,主要关注 \(b_k \sim N(\beta_k, \sigma^2((X^TX)^{-1})_{k,k})\),希望检验 \(H_0 : \beta_k =0; H_1 : \beta_k \neq 0\)。
检验统计量是 \(t^* = \frac{b_k}{s(b_k)} = \frac{b_k}{\sqrt{MSE ((X^TX)^{-1})_{k,k}}}\sim ^{H_0} t_{n-p}\),由此可以检查单个变量的显著性。注意此处所谓的显著性,指的是第 \(k\) 个变量最后一个进入模型时的显著性,无论它在 R table 里排列在哪里。和 general linear test 的结果一致。如果这一检验体现出来变量 \(X_k\) 不显著,绝大多数情况下是可以不保留的。
\(100(1-\alpha) \%\) 置信区间是 \((b_k \pm t_{1-\alpha /2,n-p} s(b_k))\),注意 \(s(b_k)\) 的含义在上述已经提到。
关于 \(E(Y_h)\) 的推断和 CI,考虑 \(\mu_h = E(Y_h) = X_{h} \beta\)。
其估计量是 \(\hat \mu_h = X_h b = X_h (X^TX)^{-1} X^TY \sim N(\mu_h , \sigma^2 X_h (X^TX)^{-1} X_h^T)\),于是 \(s^2(\hat \mu_h) = MSE \cdot X_h (X^TX)^{-1} X_h^T\)。因此 \(\mu_h\) 的 \(100 (1-\alpha) \%\) 置信区间是 \((\hat \mu_h \pm t_{1-\alpha /2 , n-p} s(\hat \mu_h))\)
考虑 \(Y_h = X_h \beta + \varepsilon\),有 \(\hat Y_h - Y_h \sim N(0,\sigma^2 + \sigma^2 X_h (X^TX)^{-1} X_h^T)\), \(s^2(\hat Y_h - Y_h) = MSE \cdot (1+X_h (X^TX)^{-1} X_h ^T)\),因此 \(Y_h\) 的 \(100 (1-\alpha) \%\) 置信区间是 \((\hat Y_h \pm t_{\alpha /2 , n-p} s(\hat Y_h - Y_h))\)
Lecture 9
Extra Sum of Squares
想法很简单,定义就是把一个新的变量加入模型后可以额外解释的方差,例如模型中本来存在 \(X_2\) 时,加入 \(X_1\) 后可以额外解释的方差是 \(SSR(X_1 | X_2) = SSR(X_1 ,X_2) - SSR(X_2) = SSE(X_2) - SSE(X_1,X_2)\)。
在多重回归中分解 sum of squares 的方式最常见的是 Type I method:
\(SSR(X_1,X_2,X_3,X_4) = SSR(X_1) + SSR(X_2 |X_1) + SSR(X_3 |X_1,X_2)+SSR(X_4 |X_1,X_2,X_3)\)
也就是所谓的 sequential sum of squares 的方法,在
anova() 中的列表就是这样的分解方式,分掉了所有的 SSR。
SAS 中的 sum of square 分解有三种模式,以考虑 A,B,AB 三种因子(2-way ANOVA)的情况如下排列:

可以看到 type I 就是按照 sequential 的模式进入模型,认为不同的变量有重要性的排序,先进入理论上来说最有必要进入模型的 A,再进入 B,最后进入 AB,分别计算 extra sum of squares;type II 忽略了交互效应 AB,对于 A 和 B 的单变量分解是与 type I 相同的;type III 和之前提到的 t 检验类似,每个模型的 extra sum of square 分解都是考虑它最后一个进入模型时带来的方差解释能力,但这里实际上存在一个问题,按照 hierarchy 的原则来说如果主效应 A,B 之一不显著/没有进入模型,是不能允许交互项 AB 进入模型的。
General Linear Test
Test Reduced Model
一种检验 full model 和 reduced model 之间关系的检验方法,例如对于存在五个变量 \(X_1,X_2,X_3,X_4,X_5\) 的 full model 和存在三个变量 \(X_1,X_2,X_3\) 的 reduced model 来说,假设 \(H_0: \beta_4 = \beta_5 = 0; H_1:\beta_4,\beta_5\) 中至少有一个不是 \(0\)。
检验统计量是 \(F^* = \frac{(SSE(R) - SSE(F))/(df_E(R) - df_E(F)}{SSE(F)/df_E(F)}\sim ^{H_0} F_{df_E(R)-df_E(F),df_E(F)}\),注意第一个自由度实际上是两个模型相差的变量个数,分母中的 \(SSE(R) - SSE(F) = SSR(F) - SSE(R) = SSR(X_4,X_5|X_1,X_2,X_3)\) 实际上是 extra sum of squares。
事实上我们是 prefer 接受 \(H_0\) 的,就相当于可以使用变量更少的模型,解释性更强;但是有的时候检验做出来接受 \(H_0\),也需要考虑一下是不是数据量太小导致 power 不够,如果数据量够大就可以放心地使用 reduced model 了。
Test Linear Hypothesis
实际上只要是关于回归系数的线性检验就都可以用 general linear test 来进行,比如 \(H_0 : \beta_1 + 3 \beta_2 =12\),等等。
\(H_0 : C \beta =t\),\(C\) 是有关 \(\beta\) 的约束条件的矩阵,检验统计量是 \(F = \frac{(C \hat \beta - t)^T (C(X^TX)^{-1} C^T)^{-1} (C \hat \beta - t)}{qs^2} \sim^{H_0} F_{q,n-p}\),其中 \(q=rank(C)\)。
偏决定系数 & 偏相关系数
\(R^2_{Yk|1,2,...,k-1,k+1,...,q} = \frac{SSR(X_k | X_1,..,X_{k-1},X_{k+1},...,X_q)}{SSE(X_1,...,X_{k-1},X_{k+1},...,X_q)} = 1- \frac{SSE(X_1,X_2,...,X_q)}{SSE(X_1,...,X_{k-1},X_{k+1},...,X_q)}\)
本质上说的是,模型中新进入的 \(X_k\) 带来的 extra sum of squares 解释了 SSE 的比例,也即解释了没有由原来的变量解释掉的方差比率。
实际上另一种表现形式可以是,我们认为 \(R^2_{Yk|1,2,...,k-1,k+1,...,q} = \frac{SSE(R)-SSE(F)}{SSE(R)} = \frac{SSR(X_k |X_{-k})}{SST(Y|X_{-k})} = R^2(Y|X_{-k}, X_k|X_{-k})\)
也就是说,实际上是对于 \(Y|X_{-k} \sim X_k|X_{-k}\) 这两组残差做线性回归,得到的决定系数正好是 \(X_k\) 的偏决定系数。
实际上偏相关系数 \(r_{k|1,2,...,k-1,k+1,...,q} = sign(\hat \beta_k)\sqrt{R^2_{Yk|1,2,...,k-1,k+1,...,q}}\) 表征的就是这两组残差之间的相关系数,如果有 \(0 < r_{3|12} < r_{12}\) 就说明变量 \(X_3\) 可以部分解释 \(X_1,X_2\) 之间的相关性。
标准回归
Motivation
- 如果 \(X_1,X_2\) 之间的尺度差距过大会导致 \(\beta_1,\beta_2\) 的尺度也有差距,无法直接比较,也可能会影响变量显著性。
- 会导致 designed matrix 接近不满秩,计算逆矩阵出现问题。
Method——Correlation Transformation
考虑 \(s_Y = \sqrt{\frac{\sum_i (Y_i - \bar Y)^2}{n-1}}, s_{X_k} = \sqrt{\frac{\sum_i (X_{ik}-\bar X_k)^2}{n-1}}\),对变量和响应值分别做标准化:
\[\begin{aligned} \frac{1}{\sqrt{n-1}} \frac{Y_i - \bar Y}{s_Y}& = \frac{1}{\sqrt{n-1}} \frac{(\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \varepsilon_i)-(\beta_0 + \beta_1 \bar X_1 + \beta_2 \bar X_2 + \bar \varepsilon)}{s_Y}\\&=\frac{1}{\sqrt{n-1}}\frac{\beta_1(X_{i1} - \bar X_1) + \beta_2 (X_{i2}-\bar X_2) + (\varepsilon_i - \bar \varepsilon)}{s_Y}\\&=\frac{\beta_1 s_{X1}}{s_Y} \frac{(X_{i1}-\bar X_1)}{\sqrt{n-1} s_{X1}} + \frac{\beta_2 s_{X2}}{s_Y} \frac{(X_{i2}-\bar X_2)}{\sqrt{n-1} s_{X2}} + \frac{\varepsilon_i - \bar \varepsilon}{\sqrt{n-1}s_Y} \end{aligned}\]
\[Y_i^* = 0 + \beta_1^* X_{i1}^* + \beta_2^* X_{i2}^* + ... +\beta_{p-1}^* X_{i,p-1}^* + \varepsilon_i\]
其中 \(\beta_k ^* = \frac{s_{X_k}}{S_Y} \beta_k\) 是新的回归系数。
注意这个方法是有一些问题的,比如说破坏了残差的假设,以及强迫过原点。
标准回归的系数估计和 ANOVA table 都发生了改变,这是因为 SST 变成了 \(1\),ANOVA table 自然会变化。但是偏决定系数都是由偏相关系数直接决定的,所以没有变化。
类似地,如果只对 \(X\) 做变换而不改变 \(Y\),会有系数发生改变,但是 ANOVA table 和偏决定系数都不变。
Suppressor Variable
如果有 \(SSR(X_2 |X_1) > SSR(X_2)\),也就是 \(X_1\) 在模型里的时候会让 \(X_2\) 更显著,则称 \(X_1\) 是一个 suppressor variable。原理是 \(X_1\) 可以帮助解释一部分 \(X_2\) 中的噪音,使得 \(X_2\) 更显著。
\(X_1\) 本身未必是显著的,这也就说明了如果单一变量不显著的话也不能贸然扔掉,它可能会是一个抑制变量。更极端的情况下,假设 \(X_1\) 和 \(Y\) 完全无关,有 \(X_2\) 在模型中不会改变 \(X_1\) 的系数估计,但是会导致 \(R^2_{Y2|1} \neq R^2_{Y2}\)。
一般来说脑补一下这种类似韦恩图的直观解释就好。
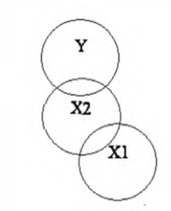
Lecture 10
Multicollinearity
关于多重共线性的一些研究,先考虑一些极端情况,然后观察多重共线性会导致什么后果。
Zero Collinearity
在几个解释变量完全没有共线性的情况称为正交设计,也就是说设计矩阵的各列之间是正交的。这是一个很好的情况,互相之间并不会干扰,有 \(X^TX = diag(||X_0||^2 , ||X_1||^2,...,||X_{p-1}||^2)\),且有 \(b_j = \frac{X_j ^TY}{||X_j||^2}\),\(Var(b_j) = \frac{\sigma^2}{||X_j||^2}\)。
结果就是无论进多少变量都不会影响单个 \(b_j\) 的估计,但是会影响到 \(MSE\) 导致 p-value 的变化。与此同时 type I, II, III ANOVA table 的结果是一样的,这是因为 extra sum of squares 就是单个变量能解释的方差。
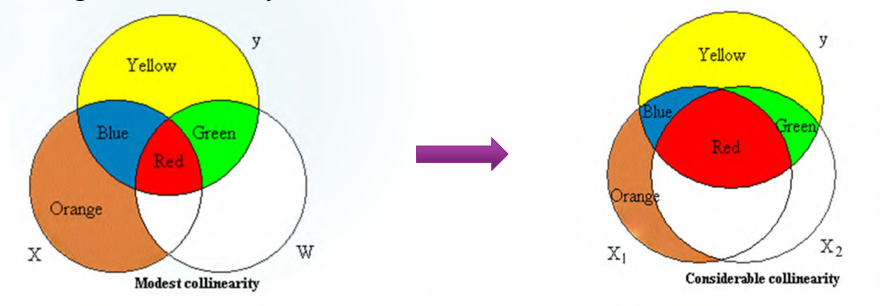
Linearly Dependent
一个比较极端的例子是完全线性相关,比如变量之间有 \(c_1 X_1 + ... +c_{p-1}X_{p-1}=c\) 这样的关系,会导致设计阵不满秩无法求逆。从数学上来说只要去掉其中一个变量即可,但是在统计上未必合适的。
Multicollinearity
正常一些的情况就是普通的多重共线性,从回归结果来看多重共线性的一大特征就是模型整体显著,但是没有一个变量是显著的。回归结果的显著性是代表每个变量最后一个进入模型时的显著性,也就是说明每个变量几乎都是可以被前面进入模型的变量表示出来的。多重共线性有以下危害:
- \(X_1,X_2\) 之间较大的多重共线性会导致对于单个变量的 \(Var(b_i)\) 增大,但是仍然是无偏估计。这也就说明了,出现多重共线性时 \(b_i\) 的方差很大,会导致 \(b_i\) 的估计值并不准确。举个例子来说,有的时候理论上 \(X_i\) 和 \(Y\) 之间是正相关,但是得到的系数估计是负的,就有可能是因为 \(Var(b_i)\) 过大导致一组数据得到的结果距离“真实值”有很大的偏差,甚至从正相关变成了负相关。
- Type I SS 和 Type II SS 的结果可能是不同的,因为变量之间对方差解释有竞争,也可能有 suppressor variable,进入模型的顺序在此时变得重要了起来,二者不同的结果可能导致判断上的问题。
- 两部分解释变量解释了同一部分的方差,导致模型解释能力下降。模型整体显著但每一个变量都不显著,很有可能是过拟合了。
- 从数学上来说 \(X^TX\) 接近退化,求逆时导致数值误差增大。
有一些弥补的方案,但是要视建立模型的目的而定:
如果单纯是为了预测,其实增大模型的 sample size 是可以解决问题的
如果是为了解释性,需要做很多其他的努力,比如移除一些变量,对变量做变换,PCA 方法等等。
仍然存在很多问题,比如移除变量时万一移除了某个重要的类别型变量,可能会导致 Simpson's Paradox 出现,移除变量也会导致系数估计的方差减小,可能减小 MSE 但是会导致 bias 增大,但如果移除了一个重要的解释变量会导致它进入 error term,进而导致 \(\sigma^2\) 的估计增大,需要 trade-off;
做变换不一定能成功降低共线性还会造成解释上的困难,PCA 的解释性更差,等等。
Multicollinearity 可能有以下来源:
- 抽样时 \(X\) 的区域太小
- 理论上两个变量就是相关的却一起放进了模型,比如家庭收入和房屋面积
- 使用多项式回归
- \(p>n\)
- 某些变量彼此是受同一隐含的因素影响的,比如一些 time series data
Polynomial Regression
多项式回归可能会导致很强的共线性,比如一个只取 \(0\) 和 \(1\) 的类别型变量取 \(x\) 和 \(x^2\)进入模型就完全共线。
有一个弥补的方案就是使用 centered data,为每一个变量减去一个均值,导致数值有正有负,再做非负的平方项就得到共线性不那么强的两个解释变量。实际上再进一步对数据做尺度上的标准化也可以,但是对系数估计没有任何影响。
对数据做中心化不会导致高阶项的系数改变,但有可能会导致低阶项的系数和 extra sum of squares 变化。另外如果显著性不随之变化的话也有可能是出现了正交设计的情况,需要按照结果分析。
交互项
模型中存在交互项的本质就是 \(X_i\) 对于 \(Y\) 的效应和回归系数估计都会受到 \(X_j\) 的影响。
如果 \(X_2\) 是连续型变量而 \(X_1\) 是类别型变量,回归模型中包含二者的交互项,例如:
\[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1X_2+\varepsilon\]
这就说明对于 group 1,也就是 \(X_1 = 0\) 时模型是 \(Y = \beta_0+ \beta_2 X_2 + \varepsilon\),对于 group 2 也就是 \(X_1 = 1\) 时模型是 \(Y = (\beta_0 + \beta_1 )+(\beta_2 + \beta_3)X_2 + \varepsilon\)。希望检验的问题是 \(\beta_1,\beta_3\) 是否为 \(0\) 来查看两组回归线的斜率、截距之间是否存在差异。
如果二者都是连续型变量也是类似的情况,相比之下类别型变量和连续型变量的交互效应有显著的分组意义。
Lecture 11
模型选择方法
一些没那么数学的
- 喜闻乐见的穷举,可惜只能处理不超过 \(n=40\) 个变量的情况
- stepwise greedy method,不喜闻乐见的要写代码,理解 idea 就好(心虚
一些准则
假设可供选择的 explanatory variable 有 \(P-1\) 个,从中选择 \(p-1\) 个并进行判断。
观察 \(R^2\) 和 adjusted \(R^2\),取后者较大的模型
观察 mallow's \(C_p\),\(\Gamma_p = \frac{E(SSE(p))}{\sigma^2} - (n-2p) \geq p\),实际上在操作中只能取 \(\hat \Gamma_p = \frac{SSE(p)}{MSE(P)}-(n-2p)\)。
- 如果 \(\hat \Gamma_p \gg p\) 说明存在显著的误差,可能遗漏了重要的变量没有进入模型
- 如果 \(\hat \Gamma_p \ll p\) 说明过拟合了,导致 \(SSE(p) \ll MSE(P)\)
- 如果 \(\hat \Gamma_p \approx p\) 说明是 unbiased,取接近于 \(p\) 的 mallow's \(C_p\) 中最小的一个对应的模型。
实际上理论的形式对于 \(P\) 有 \(\Gamma_P =P\)。
\(AIC = n \log (\frac{SSE(p)}{n}) + 2p\),\(BIC = n \log (\frac{SSE(p)}{n}) + (\log n)p\),二者都是最小值对应的模型最合适。
注意 BIC 实际上相比 AIC 加了一个更大的惩罚在模型的变量数上,更注重解释性;一般来说有 \(BIC>AIC\)。
Predicted Residual Error Sum of Squares:\(PRESS(p) = \sum_{i=1}^n (Y_i - \hat Y_{i(-i)})^2\),实际上有 \(Y_i - \hat Y_{i(-i)} = \frac{e_i}{1-h_{ii}}\)。
取使得 \(PRESS(p)\) 最小的模型。用来观察过拟合与否。
Prediction \(R_p^2\):\(R_p^2 = 1-\frac{PRESS}{SST}\),如果模型里噪音过大,则有 \(PRESS >SST\),此时 \(R_p^2<0\) 也是可以取负值的。如果有 \(R_p^2 \ll R^2\) 则也可能是过拟合了,即使有些独立变量是显著的。
我们选择模型一般会考虑 adjusted \(R^2\),AIC 或者 mallow's \(C_p\)。
模型诊断
Partial Regression Plots
每个 \(X_i\) 都可以做出一张 partial regression plot,也即所谓的 AV-plot,实际上就是对 \(Y|X_{-i} \sim X_i|X_{-i}\) 这两部分残差互相做回归得到的图,展示了完整模型中 \(Y \sim X_i\) 之间的边际关系。也可以用来检测非线性关系、异方差问题和 outliers。
Studentized Residuals
补充在 Lecture 6 里了。
Assessing Outliers
有以下指标可以考虑:
Difference caused to fitted values:\((DFFIT)_i = \hat Y_i - \hat Y_{i(-i)} = \frac{h_{ii}}{1-h_{ii}} e_i\)
Studentized DFFIT:\((DFFITS)_i = \frac{\hat Y_i - \hat Y_{i(-i)}}{\sqrt{MSE_{-i} h_{ii}}} = t_i \sqrt{\frac{h_{ii}}{1-h_{ii}}}\)。
对于不太大的数据量,如果 \(|DFFITS|>1\) 则认为是强影响力点,大数据量时认为 \(|DFFITS|>2\frac{\sqrt p}{\sqrt n}\) 是强影响力点。
Cook's Distance:\(D_i = \frac{e_i^2}{p \cdot MSE} \frac{h_{ii}}{(1-h_{ii})^2}\),在 R 中认为某个点有强影响力的 threshold 是 \(0.5\),事实上如果一个点的 Cook's distance 分布距离其他点较远,就可以认为是强影响力点了。
Difference in Beta Estimates:\((DFBETAS)_{k(-i)} = \frac{b_k - b_{k(-i)}}{\sqrt{MSE_{(-i)} c_{kk}}}\),其中 \(c_{kk}\) 是 \((X^TX)^{-1}\) 的第 \(k \times k\) 个分量。
对于大的数据量,如果 \(|DFFITS|>1\) 则认为是对于回归系数估计值的强影响力点,不太大的数据量时认为 \(|DFFITS|>\frac{2}{\sqrt n}\) 是对于回归系数估计值的强影响力点。
Multicollinearity Diagnose
有以下两个指标:
- Variance Inflation Factor:多重共线性经常导致方差膨胀,这是一个表征的指标,\((VIF)_k = (1- R_k^2)^{-1}\),其中 \(R_k^2\) 指的是将 \(X_k\) 相对于其他 \(p-2\) 个 explanatory variable 做回归得到的决定系数。如果 \((VIF)_k \gg 1\) 则认为第 \(k\) 个变量 \(X_k\) 是会发生多重共线性的变量。
- Tolerance:\(TOL = 1/VIF\),判断准则类似上述。
Lecture 12
本节探讨 remedies for multiple linear regression,主要是异方差情况和多重共线性。
Equal Variance Remedy
这一部分主要处理模型发生异方差问题的情况。
也就是说,实际上有 \(\varepsilon_1, \varepsilon_2, ..., \varepsilon_n\) 的方差不全为 \(\sigma^2\),记方差为 \(\sigma_1 ^2,\sigma_2 ^2 , ..., \sigma_n ^2\)。此时的 likelihood function 是:
\[L(\beta_1,\beta_2) = \Pi_{i=1} ^n f_i(\beta_1, \beta_2 |X_i,Y_i) = \Pi_{i=1}^n (\frac{1}{\sqrt{2\pi} \sigma_i} exp(-\frac 1 2 (\frac{Y_i - \beta_0 -\beta_1 X_i}{\sigma_i})^2)) \]
可以看到 ordinary least square 条件得到的 \(b_0 = \hat \beta_0,b_1 = \hat \beta_1\) 不再满足 MLE 的条件。但如果是在不知异方差的情况下仍然使用 OLS 或者 MLE 条件得到的参数估计,仍然是可以满足无偏性的,但不满足最小方差性质。
Weighted Regression
简单来说,通过选取 \(\{ w_i = \frac{1}{\sigma_i ^2} \}_{i=1} ^n\) 作为权重,考虑 \(\Sigma_{i=1} ^n w_i e_i^2 = \Sigma_{i=1} ^n (\frac{Y_i - \beta_0 - \beta_1 X_{i,1} - ... - \beta_{p-1} X_{i,p-1}}{\sigma_i})^2\) 的最小性问题。
最简单的情况,\(\sigma_1,...,\sigma_n\) 均已知,则有 \(w_i = \frac{1}{\sigma_i ^2}\),
取 \(W = \begin{bmatrix} \frac{1}{\sigma_1 ^2} & & & \\ &...& & \\ & & & \frac{1}{\sigma_n^2} \end{bmatrix}\) 使得回归问题变为 \(W^{\frac 1 2} Y = W^{\frac 1 2} X \beta + W^{\frac 1 2} \varepsilon\),记 \(Y^* = W^{\frac 1 2} Y, X^* = W^{\frac 1 2} X, \varepsilon^* = W^{\frac 1 2} \varepsilon\),由于 \(Var(\varepsilon^*) = I_{n\times n}\) 满足同方差条件,因此新的回归问题是符合条件的。
注意新的回归问题 \(Y^* = X^* \beta + \varepsilon^*\) 事实上没有改变系数 \(\beta\),但系数估计 \(b_w = (X^TWX)^{-1} (X^TWY)\) 是改变了的,这是正常现象,因为对这一问题做 remedy 的主要原因就是假设不满足,导致按照 OLS 做出的系数估计不准确,因此 weighted regression 做出的修正也是相对于原系数 \(\beta\) 的。
\(b_w\) 仍然是无偏估计,也保证 \(Var(b_w) = (X^TWX)^{-1}\) 是最小方差。
稍微复杂一点的情况,虽然 \(\sigma_i^2\) 未知但 \(\sigma^2_i / \sigma_j ^2\) 均已知,取 \(w_i = \frac{\sigma_1 ^2}{\sigma_i^2 }\) 即可。于是有:
取 \(W = \sigma_1 ^2 \begin{bmatrix} \frac{1}{\sigma_1 ^2} & & & \\ &...& & \\ & & & \frac{1}{\sigma_n^2} \end{bmatrix}\) 使得回归问题变为 \(W^{\frac 1 2} Y = W^{\frac 1 2} X \beta + W^{\frac 1 2} \varepsilon\),记 \(Y^* = W^{\frac 1 2} Y, X^* = W^{\frac 1 2} X, \varepsilon^* = W^{\frac 1 2} \varepsilon\),由于 \(Var(\varepsilon^*) = \sigma_1 ^2 I_{n\times n}\) 满足同方差条件,因此新的回归问题是符合条件的。
新的回归系数估计是 \(b_w = (X^TWX)^{-1}(X^TWY)\),\(Var(b_w) = \sigma_1^2(X^TWX)^{-1}\),由此还可以做出对 \(\sigma_1\) 的参数估计,\(\hat \sigma_1 ^2 = MSE_{wls} = \frac{\Sigma(Y^*_i - \hat Y^*_i)^2}{n-p}= \frac{\Sigma w_i(Y_i - \hat Y_i)^2}{n-p} = \frac{\Sigma w_i e_i ^2}{n-p}\),其中 \(w_i = \frac{\sigma_1^2}{\sigma_i^2}\)。
一般情况下 \(\{ \sigma_i \}\) 是完全未知的,我们是在模型诊断中发现异方差的现象,因此不可能直接通过方差值推权重系数。这个时候一般有两种选择:
重复试验取 \(Y_i\) 的方差估计 \(s_i^2\),于是权重系数为 \(w_i = \frac{1}{s_i ^2}\)。
先对 \(Y\sim X\) 进行 OLS 回归,取出此时的 residual \(\{e_i \}\) 作为 \(\{ \sigma _i \}\) 的估计,取 \(w_i = \frac{1}{e_i ^2}\) 作为权重即可。
效果不明显时多迭代几次。
在观察 weighted least square 和 ordinary least square 模型差别时,注意:
- \(R^2\) 以及 adjusted \(R^2\) 的数值差别没有很强的意义,WLS 情况下原始数据 \(\{ Y_i \}\) 已经发生了变化,实际上 SST 也已经变了,没有什么比较的意义。
- 需要关注的点是 residual standard error,越接近 \(1\) 越说明异方差的调整是成功的。
- 有时会观察到 WLS 情况下 \(\hat \sigma^2\) 在减小,似乎数据的分散程度在减小,这是因为 MSE 在减小。但是 WLS 和 OLS 情况下的 MSE 和 MST 都没有比较的意义,因此 \(\hat \sigma\) 的变化也没有研究的价值。唯一确定的是它会接近于 \(1\),这一点可以证明异方差的调整效果是成功的。
Multicollinearity Remedy
如果存在多重共线性,主要发生的问题是 \(X^TX\) 求逆是一个病态的数值问题,误差很大。实际上极端来说如果存在完全共线性,\(X^TX\) 会退化为不满秩的情况。
可以用 ridge regression 对多重共线性进行弥补。
Ridge Regression
主要的 idea 是如果 \((X^TX)\) 接近于不满秩,则在参数估计中将其改变为 \((X^TX +\lambda I)\),\(\lambda\) 是待取的参数。对于矩阵的对角元进行改变如同突起的山脊,因此得名岭回归。
Ridge regression 的本质是对优化问题进行了修改。OLS 中的优化问题是求使得 \((Y-X\beta)^T (Y-X\beta)\) 最小的 \(\beta\),ridge regression 中将 \(|| \beta ||_2 ^2 = \Sigma_{i=0} ^{p-1} \beta_i^2\) 加入了优化,对 \(\beta\) 的长度(事实上应该称之为 2- 范数)做惩罚。因此,实际上是求使得 \((Y-X \beta )^T (Y-X \beta) + \lambda \Sigma_{i=0} ^{p-1}\beta_i ^2\) 最小的 \(\hat \beta = (X^TX + \lambda I)^{-1} X^TY\),这使得参数估计 \(b = \hat \beta\) 呈现出比 OLS 下长度和方差都更小的特征。
在实际应用中,需要通过确定最佳的 \(\lambda\) 从而得到合适的参数估计,一般是对 \(\lambda\) 取一个 sequence 进行尝试。如果发现某个 explanatory variable 的系数在 \(\lambda\) 增大时很快下降到 \(0\),实际上它很有可能是不需要进入模型的。
应用岭回归来弥补模型的多重共线性的时候,既是为了消除共线性,也是在牺牲一些 \(\hat \beta\) 的无偏性来换取更小的方差。
LASSO & Elastic Net
LASSO 中把惩罚的 \(\beta\) 长度替换为了 \(\beta\) 的 1- 范数,弹性网络则是对 LASSO 和 ridge regression 进行了结合。
本质上都是 Bayesian modes。
Influencial Cases Remedy
更改一些更 robust 的优化模型,例如 least absolute deviation 和 least median of squares,缺点是算起来会比较困难。
或者考虑非参数模型。
Nonlinearity Remedy
考虑局部多项式回归/局部回归,总之是对数据进行分块,所谓的 lowess。
Lecture 13
One Factor ANOVA
(从生统笔记复制来的)
首先给出一个希望做检验的场景:\(n_T\) 个实验对象被分成 \(r\) 组,每组有 \(n_i\) 个实验对象,有 \(n_T = \Sigma_{i=1} ^r n_i\)。由此我们得到 \(n_T\) 个数据 \(Y_{ij}\),\(i\) 表示组别,\(1\leq i \leq r\),\(j\) 表示在某一组内的编号,\(1 \leq j \leq n_i\)。
Cell means model
模型假设是 \(Y_{ij} = \mu_i + \varepsilon_{ij}\)。
其中,\(\mu_i\) 是第 \(i\) 组的理论均值,\(\varepsilon _{ij}\) i.i.d. \(\sim N(0,\sigma^2)\)。注意到在这一模型假设中有 \(r+1\) 个参数,分别是 \(\mu_1,\mu_2,...,\mu_r,\sigma^2\),我们需要用得到的数据来对这些未知参数进行估计。考虑一些统计量作为参数的估计量:
\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 }^{n_i} Y_{ij} = \hat \mu _i\]
\[\bar{Y}_{..} = \frac{1}{n_T} \Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r n_i \bar{Y}_{i.}\]
\[s_i ^2 = \Sigma_{j=1} ^{n_i} (Y_{ij} - \bar Y_{i.})^2 / (n_i -1) \]
\[s^2 =\Sigma_{i=1} ^r \Sigma_{j=1} ^{n_i} (Y_{ij} - \bar Y_{i.})^2 =\frac{1}{n_T- r} \Sigma_{i=1}^r (n_i -1) s_i ^2 = \hat \sigma^2\]
在这一模型中,我们关注的假设检验是 \(i\) 组实验之间是否存在差异,假设检验表示为 \(H_0 : \mu_1= \mu_2 = ... = \mu_r = \mu\),对应的备择假设即为 \(\{ \mu_i \}_{i=1} ^r\) 中存在不同的项。检验最经典的方法即为 ANOVA,analysis of variance。核心是以下的分解:
\[\begin{aligned} SSTO = \Sigma_i \Sigma_j(Y_{ij} - \bar Y_{..})^2 &= \Sigma_i \Sigma_j (Y_{ij} - \bar Y_{i.} +\bar Y_{i.} - \bar Y_{..})^2 \\& = \Sigma_i n_i (\bar Y_{i.} - \bar Y_{..})^2 + \Sigma_i \Sigma_j (Y_{ij} - \bar Y_{i.})^2 \\ &=SSTR + SSE \end{aligned}\]
可以观察到,\(SSTR\) 是组间差距,体现了不同组别之间的差别,\(SSE\) 是组内差距,体现了同一组内各数据的偏差。注意 \(SSTR\) 的自由度是 \(r-1\),\(SSE\) 的自由度是 \(n_T - r\),\(SSTO\) 的自由度是 \(n_T - 1\)。
两个统计量的期望是 \(\mathbb E(MSE) = \sigma^2\),\(\mathbb E(MSTR) = \sigma^2 +\frac{\Sigma_i n_i (\mu _i -\mu_.)^2}{r-1}\),其中 \(\mu_. = \frac{\Sigma_i n_i \mu_i}{n_T}\)。
在 \(H_0\) 成立时,\(\frac{SSE}{\sigma^2} \sim \chi^2 _{n_T - r}\),\(\frac{SSTR}{\sigma^2} \sim \chi^2_{r-1}\)。因此 \(F=\frac{MSTR}{MSE} \sim F_{r-1,n_T -r}\) 作为最终的检验统计量。
当 \(F^* > F(1-\alpha , r-1 , n_T -r)\) 时拒绝原假设,否则接受;\(Power = P(F^* > F(1-\alpha , r-1,n_T -r)| \delta)\),其中 \(\delta\) 是一个非中心偏移量,\(\delta = \frac{1}{\sigma} \sqrt{\frac 1 r \Sigma_i n_i (\mu_i - \mu_.)^2}\)。
也可以作为一个线性回归的问题来看待,design matrix 是 $ X =
\[\begin{bmatrix} 1 & 0 & 0 & ... & 0 \\ 0 & 1 & 0 & ... & 0 \\ ... &...&...&...&... \\ 0 & 0 & 0 & ... & 1 \end{bmatrix}\]$,系数向量是 \(\mu = \begin{bmatrix} \mu_1 \\ \mu_2 \\ ... \\ \mu_r \end{bmatrix}\),因此整体的回归方程是 $ Y = X + $,注意这个回归问题是强迫过原点的。
Factor Effects Model
Factor Effects Model 是 Cell Means Model 的一个重新参数化的结果。模型假设是 \(Y_{ij} = \mu + \tau_i + \varepsilon_{ij}\)。
其中,\(\mu_i\) 是整体的理论均值,\(\varepsilon _{ij} i.i.d. \sim N(0,\sigma^2)\)。它的参数比 cell mean model 多一个,分别是 \(\mu , \tau_1 , ..., \tau_r , \sigma^2\),但是自由度是相同的,因为 \(\{ \tau _i \}_{i=1}^r\) 存在一个约束 \(\Sigma_{i=1}^r \tau_i = 0\),如果没有这个约束会导致存在多组解。考虑一些统计量作为参数的估计量:
\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 }^{n_i} Y_{ij} = \hat \tau _i + \hat \mu\]
\[\bar{Y}_{..} = \frac{1}{n_T} \Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r n_i \bar{Y}_{i.} = \hat{\mu}\]
\[s_i ^2 = \Sigma(Y_{ij} - \bar Y_{i.})^2 / (n_i -1) \]
\[s^2 = \frac{1}{n_T- r} \Sigma_{i=1}^r (n_i -1) s_i ^2 = \hat \sigma^2\]
在这一模型中,我们关注的假设检验仍然是 \(i\) 组实验之间是否存在差异,假设检验表示为 \(H_0 : \tau_1= \tau_2 = ... = \tau_r = 0\),对应的备择假设即为 \(\{ \mu_i \}_{i=1} ^r\) 中存在不同的项。factor effects model 在参数的含义上比 cell mean model 更清晰。
可以作为一个线性回归的问题来看待,design matrix 是 $ X =
\[\begin{bmatrix} 1 & 1 & 0 & ... & 0 \\ 1 & 0 & 1 & ... & 0 \\ ... &...&...&...&... \\ 1 & -1 & -1 & ... & -1 \end{bmatrix}\]$,系数向量是 \(\mu = \begin{bmatrix} \mu \\ \tau_1 \\ \tau_2 \\ ... \\ \tau_{r-1} \end{bmatrix}\),因此整体的回归方程是 $ Y = X + $,注意这个回归问题的截距就是 \(\mu\),不强迫过原点,相比 cell mean model 算是做了一点点优化。
Example
在做回归之前要注明哪些变量是 factor:
1
2
3
4> data$design = factor(data$design)
> fit = lm(cases ~ design, data = data)
> summary(fit)方便查看 \(\hat \mu_i\) 的命令是过原点回归,但查看 MSR 的方式是不过原点回归。
\(Std.Error_i ^2 = Var(\hat \mu_i) = Var(\frac{\Sigma_{j=1}^{n_i} Y_{ij}}{n_i}) = \frac{\hat \sigma^2}{n_i}= \frac{s^2}{n_i}\)
\(sd_i ^2 = s_i ^2\),由此计算出 \(s^2\) 后再得到每个 \(Std.Error\) 的值是 \(\frac{s}{\sqrt n_i}\)。
Inference on One-Way ANOVA
Confidence Interval for \(\mu_i\)
事实上这只是个理论上可做的问题而已,现实中不会对 \(\mu_i\) 做推断,我们关注的是 \(\mu_i\) 之间的差异。
由于 \(\bar Y_{i.} \sim N(\mu_i , \sigma^2 / n_i)\),因此 \(\mu_i\) 的 pooled confidence interval 是 \((\bar Y_{i.} - t_c \frac{s}{\sqrt n_i} , \bar Y_{i.} + t_c \frac{s}{\sqrt n_i})\),其中 \(t_c = t(1-\frac{\alpha}{2}, n_T -r)\)。注意其中的 \(s^2\) 在上面已经有定义,实际上就是 SSE。
当然也可以认为是 \((\bar Y_{i.} - t_c s_i , \bar Y_{i.} + t_c s_i)\),\(s_i\) 是每个 \(\mu_i\) 对应的 \(sd_i\)。但是这样得到的置信区间一般来说较宽,准确性不如 pooled confidence interval,我们不太会采用。
实际上这样做 t-test 的话 family-wise error rate 很大,即使做出显著的效果也很有可能是发生了 Type I Error。
Bonferroni Confidence Intervals for \(\mu_i\)
想要同时估计所有的 \(\mu_i\) 的时候可以采用 Bonferroni method,但是也有明显的缺点是一旦 factor level \(r\) 较大,就会导致每个 \(\mu_i\) 都不显著,置信区间的 level of significance 只有 \(\alpha / 2r\),几乎是无效的。
同样是 t-test,但过于保守了。对于较小的 \(r\) 可以进行尝试。
Test Difference in Means
由于 \(\bar Y_{i.} - \bar Y_{j.} \sim N(\mu_i - \mu_k , \frac{\sigma^2}{n_i} + \frac{\sigma ^2}{n_j})\),\(\mu_i - \mu_k\) 的 confidence interval 是 \((\bar Y_{i.} - \bar Y_{j.}-t_c s(\bar Y_{i.} - \bar Y_{k.}), \bar Y_{i.} - \bar Y_{j.}+t_c s(\bar Y_{i.} - \bar Y_{k.}))\),其中 \(s(\bar Y_i. - \bar Y_k.) = \sqrt{\frac{\hat \sigma^2}{n_i} + \frac{\hat \sigma^2}{n_j}} = s \sqrt{\frac{1}{n_i} + \frac{1}{n_j}}\),\(t_c\) 是和检验方法有关的常数。
由于一共有 \(r\) 个 mean \(\mu_i\),所以一共要做 \(\frac{r(r-1)}{2}\) 次检验来确定两两之间有无差异。
- Tukey's HSD Method: 使用 q-test,取 \(t_c = \frac{\bar y _{max} - \bar y_{min}}{\sqrt 2 s /\sqrt n}\);适用于两两检验。
- Scheffe's Method: 使用 F-test,取 \(t_c = \sqrt{(r-1)F(1-\alpha, r-1, n_T -r)}\),适用于线性组合的对照(contrast,见下)。实际上也过于保守了,导致 power 比较低。
Contrast
Concept
关于对照的具体定义是,取一组均值为 \(0\) 的常数作为权重,即为 \(\Sigma_{i=1} ^r c_i =0\),此时研究 \(L = \Sigma_{i=1} ^r c_i \mu_i\) 的推断。
注意到 \(\hat L = \Sigma c_i \bar Y_i . \sim N(L, Var(\hat L))\),其中 \(Var(\hat L) = \Sigma c_i ^2 Var(\bar Y_i .)\),\(\hat Var (\hat L) = MSE \Sigma( c^2_i / n_i)\)。
test statistic 是 \(T= \frac{\hat L - L_0}{\sqrt{\hat Var(\hat L)}} \sim t(n_T-r)\)。例如在 \(H_0 : L =0\) 下有 \(T = \frac{\Sigma c_i \bar Y_i .}{\sqrt{MSE \Sigma c^2_i / n_i}} \sim t(n_T -r)\),于是 \(T^2 = \frac{(\Sigma c_i \bar Y_i.)^2}{MSE \Sigma c_i^2 /n_i} = \frac{SSC/1}{MSE} \sim F(1,n_T-r)\),其中定义 \(SSC = (\Sigma c_i \bar Y_i.)^2 / \Sigma (c_i^2/n_i)\),称为 sum of contrast。
Multiple Contrasts
可以利用 R 同时检验若干组 contrast,比如同时检验 \(\mu_1 = \mu_2, \mu_3 = \mu_2 , \mu_1 =( \mu_1 + \mu_2+\mu_3 )/ 3\)
实际上 linear hypothesis test 和 multiple comparison 的主要差别在于自由度,比如说对于 \(\mu_1 = \mu_2 = \mu_3\) 做检验,前者会将其拆成两个两两检验,自由度是 \(2\),后者会作为一个整体的 contrast,自由度是 \(1\)。
Lecture 14
依旧来自生统概论的笔记。
Two-Way ANOVA
首先给出一个希望做检验的场景:\(nab\) 个实验对象被分成 \(a\times b\) 组,每组有 \(n\) 个实验对象。第 \(ij\) 组的实验条件是 \(A\) 因素的等级为 \(i\),\(B\) 因素的等级为 \(j\),其中有 \(1 \leq i \leq a, 1\leq j \leq b\)。由此我们得到 \(nab\) 个数据 \(Y_{ijk}\),\(i\) 表示以 \(A\) 因素分类的组别,\(j\) 表示以 \(B\) 因素分类的组别,\(k\) 表示在某一组内的编号,\(1 \leq k \leq n\)。
每一组都是 \(n\) 个人,这是一个 balanced design。
Cell Mean Model
模型假设是 \(Y_{ijk} = \mu_{ij} + \varepsilon_{ijk}\)。
其中,\(\mu_{ij}\) 是第 \({i \times j}\) 水平的均值,\(\varepsilon_{ijk}\) i.i.d. \(\sim N(0,\sigma^2)\),模型中实际上有 \(ab+1\) 个未知参数需要估计。
\(\mu_{ij}\) 的估计量是 \(\bar Y_{ij.} = \sum_k Y_{ijk} /n\),对于 \(i \times j\) 水平的方差估计是 \(s_{ij}^2 = \sum_k (Y_{ijk} - \bar Y_{ij.})^2 / (n-1)\)。但是想要估计 \(\sigma^2\) 时必须要将所有的数值加权 pool 起来做估计,是 \(s^2 = \sum_{ij} (n_{ij}-1) s_{ij} ^2 / \sum_{ij} (n_{ij}-1)\),注意到如果是 balanced test 的情况实际上就是 \(s^2 = \sum_{ij} s^2_{ij} / ab\) 直接做平均的结果。更倾向于 pooled \(s^2\) 是因为自由度更大,数据利用更充分。
直接通过看图来观察两个因子之间是否存在交互效应、单因子是否显著这件事的时候,比较经典的情况就是以下两种:
上面第一张图中可以发现两条回归线之间存在斜率的差异,说明 B 因子对于 A 因子的效果存在影响,也就是存在交互效应;在 \(b_2\) level 上 A 因子是不显著的,但在 \(b_1\) level 上 A 因子显著;同理在 \(a_1\) level 上 B 因子不显著,但在 \(a_2\) level 上 B 因子显著。实际上在这个情况下交互效应显著,主效应虽然显著但也没有太大意义了,不过想要解释也是可以的,可以认为 A 因子带来的效应至少不是负效应。
第二张图里更有两条回归线交叉,存在斜率的差异,交互效应显著;但主效应此时可能无法解释,尤其是如果两条回归线完全交叉成 \(\times\) 形状,A 因子会在不同的 B 因子条件下起到相反的作用。所以一般是认为交互效应显著时主效应显著,但没有解释意义。显著性和解释性之间无关。
在读 R code 的时候直接把所有的 estimation 读作 factor effect model 的系数,再代回就可以理解系数的来源了。这一部分在 factor effects model 里详述。
Factor Effects Model
模型假设是 \(Y_{ijk} = \mu +\alpha_i + \beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) 表示和两个因素同时相关的变化,相当于一个交叉项。
这里面有 \((a+1)(b+1)\) 个参数,对其也有一定的约束:\(\Sigma_i \alpha_i = \Sigma_j \beta_j = \Sigma_i (\alpha \beta)_{ij} = \Sigma_j (\alpha \beta)_{ij} =0\),事实上有 \(a+b-1\) 个关于交互效应的约束,有 \(2\) 个关于单因子效应的约束,实际上包含 \(\sigma^2\) 后仍然是有 \(ab+1\) 个参数。做一些其他的参数假设,让参数含义更清晰:
\[\mu_{i.} = \alpha_i +\mu_{..}\]
\[\mu_{.j} = \beta _j + \mu_{..}\]
\[\mu_{ij} = \mu_{..} +\alpha_i + \beta_j +(\alpha \beta)_{ij}\]
如果 \((\alpha \beta)_{ij}=0\) 则说明因素 \(A,B\) 之间不存在相互作用的关系,这样的模型称为 additive model。
考虑一些统计量作为参数的估计量:
\[\bar{Y}_{ij.} = \frac{1}{n} \Sigma_{k=1 }^{n} Y_{ijk} = \hat \mu_{ij} = \hat \mu + \hat \alpha _i + \hat \beta_j + \hat{(\alpha \beta)}_{ij}\]
\[\bar{Y}_{i..} = \frac{1}{bn} \Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \alpha_i = \hat \mu_{i.}\]
\[\bar{Y}_{.j.} = \frac{1}{an} \Sigma_{i=1}^a \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \beta_j = \hat \mu_{.j}\]
\[\bar{Y}_{...} = \frac{1}{abn}\Sigma_{i=1}^a \Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} \]
Two factors ANOVA 的方差分解更复杂一些:
\[\begin{aligned} SSTO &= \Sigma_i \Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{...})^2 \\ &= \Sigma_i \Sigma_j \Sigma_k ((\bar Y_{i..} - \bar Y_{...})+(\bar{Y}_{.j.} - \bar Y_{...}) +(\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...}) +(Y_{ijk} - \bar Y_{ij.}))^2 \\&=bn\Sigma_i (\bar Y_{i..} - \bar Y_{...})^2+an\Sigma_j (\bar{Y}_{.j.} - \bar Y_{...})^2+n\Sigma_i \Sigma_j (\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...})^2+ \Sigma_{i}\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{ij.})^2 \\&=SSA +SSB+SSAB+SSE \end{aligned}\]
其中,\(SSA\) 的自由度是 \(a-1\),\(SSB\) 的自由度是 \(b-1\),\(SSAB\) 的自由度是 \((a-1)(b-1)\),\(SSE\) 的自由度是 \(ab(n-1)\),\(SSTO\) 的自由度是 \(abn-1\)。在这一个复杂问题中我们关心不同的问题,可以做出三种不同的假设检验,有对应的检验统计量。
- \(A\) 因素是否会导致差异?\(H_0: \alpha_1 =\alpha_2=...=\alpha_a\),在 \(H_0\) 下有 \(F^* = \frac{SSA/(a-1)}{SSE/(ab(n-1))} \sim F_{a-1,ab(n-1)}\)
- \(B\) 因素是否会导致差异?\(H_0: \beta_1 =\beta_2=...=\beta_b\),在 \(H_0\) 下有 \(F^* = \frac{SSB/(b-1)}{SSE/(ab(n-1))} \sim F_{b-1,ab(n-1)}\)
- \(A,B\) 是否联合作用?\(H_0:(\alpha \beta)_{ij}=0, \forall 1 \leq i \leq a,1\leq j \leq b\),在 \(H_0\) 下有 \(F^*=\frac{SSAB/(a-1)(b-1)}{SSE/(ab(n-1))} \sim F_{(a-1)(b-1),ab(n-1)}\)
不能直接用 chi-square 统计量作为检验统计量的原因是实际上 \(MSE,MSA\) 等统计量中都带有未知的 \(\sigma^2\) 参数项。
注意 \(n_{ij}\) 是相等的也就是平衡设计,所以 Type I 和 Type III ANOVA 的结果是一样的。
Two-Way ANOVA in R
模型假设是 \(Y_{ijk} = \mu +\alpha_i + \beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) 表示和两个因素同时相关的变化,相当于一个交叉项。
这里面有 \((a+1)(b+1)\) 个参数,对其也有一定的约束。R code 中的约束是和上述理论不同的,因此 estimator 的读取也并不相同,认为 \(\alpha_1 = \beta_1 = (\alpha \beta)_{1j} = (\alpha \beta)_{i1}=0\),事实上也还是 \(a+b+1\) 个约束条件,可以估计出 \(ab+1\) 个不同参数。
相应地,对应的 design matrix 也不尽相同。这里以 \(a=3,b=2,n=2\) 为例,coefficient table 如下所示:
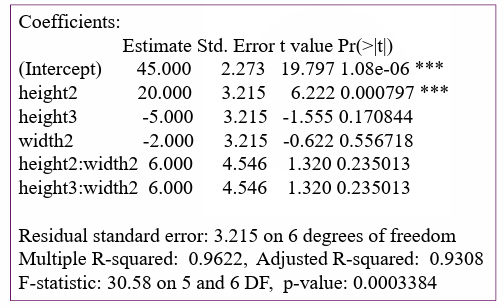
Coefficient table 里的 Intercept 代表的实际上是 \(\mu\),预设了 \(\beta_1=0\),height2 即为 \(\beta_2\),height3 即为 \(\beta_3\);预设了 \(\alpha_1=0\),width2 即为 \(\alpha_2\);关于交互效应项,由于预设了 \((\alpha \beta)_{11} = (\alpha \beta)_{12} = (\alpha \beta)_{13} =(\alpha \beta)_{21}=0\),不为零的交互效应项只有两个,分别由 height2:weight2 对应 \((\alpha \beta)_{22}\),height2:weight3 对应 \((\alpha \beta)_{23}\)。
由此我们可以依次按照 \(\mu_{ij} = \mu + \alpha_i + \beta_j +(\alpha \beta)_{ij}\) 算出所有的 \(\mu_{ij}\) 的估计量。
在这之后我们希望得到一个关于 \(12\) 个数据的设计阵,实际上就是把数据和上述分析对应起来:

Least Square Means
遇到非平衡设计,或者 covariates 的情况(连续型变量和类别性变量产生交互效应的情况),需要考虑 least square means 而不是 pooled means。简单来说 least square means 是均值的均值,达到了最小的方差,而 pooled means 就是全体数据的均值,在非平衡设计的情况下很可能引入偏差。
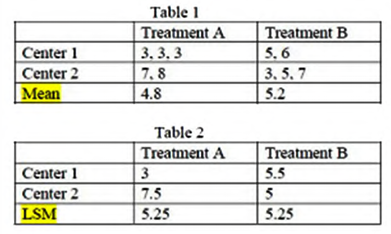
Balanced Test
对于一个平衡设计来说,它本质上是一个正交设计,模型中进一个因子还是两个因子都不会改变彼此的系数估计,只有自由度会有改变。least square mean 就是普通的 pooled mean,one-way ANOVA 和 two-way ANOVA 的结果一致。
Unbalanced Test
非平衡设计的时候 one-way ANOVA 的结果仍然是一样的,least square mean 和 pooled mean 得到的都是这一组内所有的观测值的平均。在这里就是认为 A 因子的 height1 level 的估计值是 \(\hat \mu_{1} = \frac 1 3(X_{11} +X_{12} +X_{13}) = 43\)。
但是新加入一个因子做 two-way ANOVA 就会导致 least square mean 下的系数估计发生变化,从 coefficient table 可以看出 \(\mu_{i1}\) 和 \(\mu_{i2}\) 都改变了(绷不住了,虽然并不知道是怎么变的,但是会从系数表读出每一个 \(\mu_{ij}\) 就可以了),仍然使用 \(\frac 1 2(\mu_{i1}+\mu_{i2})\) 作为 \(\mu_{i.}\) 的估计,就也会相应地发生变化。
事实上 least square mean 还可以称作 predicted mean 的原因就是,此处的 \(\mu_{11}\) 和 \(\mu_{12}\) 分别作为 \(1\times 1,1\times 2\) 这两格的预测值出现,它们的平均就作为 \(\mu_{1.}\) 这一个 A 因子的 height1 level 对应的预测值出现。在具体的例子里,此处因为得到的估计是 \(\hat \mu_{11} = 41, \hat \mu_{12} = 44\),于是认为 \(\hat \mu_{1.} = \frac 1 2 (\hat \mu_{11} + \hat \mu_{12}) = 42.5\)。
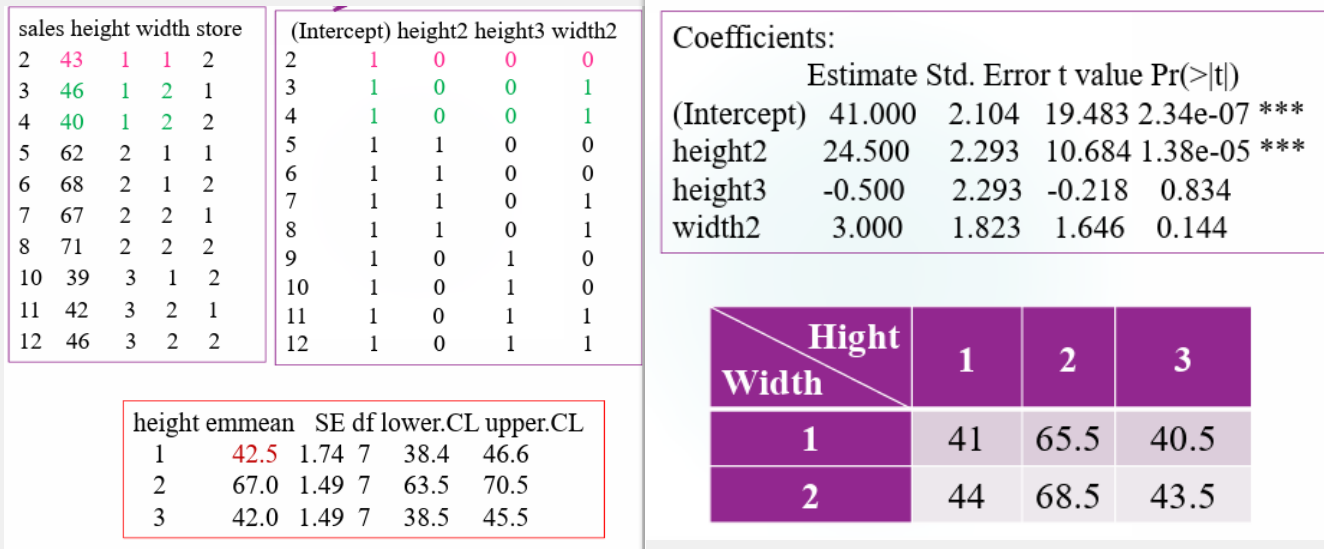
总之可以看到,unbalance test 会导致实验设计并不是正交的,B 因子的加入会对 A 因子的均值估计产生影响,这也是我们一般希望使用 balanced test 的理由。
Model Diagnose & Remedy
马上要告别应统了,于是不考也就不想学了,摆烂。
附录
常见重要分布
From Statistic Note P10, by V1ncent19
| \(X\) | \(p_X(k)\big/f_X(x)\) | \(\mathbb{E}\) | \(var\) | PGF | MGF |
|---|---|---|---|---|---|
| \(\mathrm{Bern} (p)\) | \(p\) | \(pq\) | \(q+pe^s\) | ||
| \(B (n,p)\) | \(C_n^k p^k(1-p)^{n-k}\) | \(np\) | \(npq\) | \((q+ps)^n\) | \((q+pe^s)^n\) |
| \(\mathrm{Geo} (p)\) | \((1-p)^{k-1}p\) | \(\dfrac{1}{p}\) | \(\dfrac{q}{p^2}\) | \(\dfrac{ps}{1-qs}\) | \(\dfrac{pe^s}{1-qe^s}\) |
| \(H(n,M,N)\) | \(\dfrac{C_M^kC_{N-M}^{n-k}}{C_N^n}\) | \(n\dfrac{M}{N}\) | \(\dfrac{nM(N-n)(N-M)}{N^2(n-1)}\) | ||
| \(P(\lambda)\) | \(\dfrac{\lambda^k}{k!}e^{-\lambda}\) | \(\lambda\) | \(\lambda\) | \(e^{\lambda(s-1)}\) | \(e^{\lambda(e^s-1)}\) |
| \(U(a,b)\) | \(\dfrac{1}{b-a}\) | \(\dfrac{a+b}{2}\) | \(\dfrac{(b-a)^2}{12}\) | \(\dfrac{e^{sb}-e^{sa}}{(b-a)^s}\) | |
| \(N(\mu,\sigma^2)\) | \(\dfrac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\) | \(\mu\) | \(\sigma^2\) | \(e^{\frac{\sigma^2s^2}{2}+\mu s}\) | |
| \(\epsilon(\lambda)\) | \(\lambda e^{-\lambda x}\) | \(\dfrac{1}{\lambda}\) | \(\dfrac{1}{\lambda^2}\) | \(\frac{\lambda}{\lambda-s}\) | |
| \(\Gamma(\alpha,\lambda)\) | \(\dfrac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}\) | \(\dfrac{\alpha}{\lambda}\) | \(\dfrac{\alpha}{\lambda^2}\) | \(\left(\frac{\lambda}{\lambda-s}\right)^\alpha\) | |
| \(B(\alpha,\beta)\) | \(\dfrac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\) | \(\dfrac{\alpha}{\alpha+\beta}\) | \(\dfrac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\) | ||
| \(\chi^2_n\) | \(\dfrac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}\) | \(n\) | \(2n\) | $ (1-2s)^{-n/2} $ | |
| \(t_\nu\) | \(\dfrac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu\pi}\Gamma(\frac{\nu}{2})}(1+\frac{x^2}{\nu})^{-\frac{\nu+1}{2}}\) | \(0\) | \(\dfrac{\nu}{\nu-2}\) | ||
| \(F_{m,n}\) | \(\dfrac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{m}{2})\Gamma(\frac{n}{2})}\dfrac{m^\frac{m}{2}n^\frac{n}{2}x^{\frac{m}{2}-1}}{(mx+n)^{\frac{m+n}{2}}}\) | \(\dfrac{n}{n-2}\) | \(\dfrac{2n^2(m+n-2)}{m(n-2)^2(n-4)}\) |
Consider \(X_1,X_2,\ldots,X_n\) i.i.d. \(\sim N(0,1)\); \(Y,Y_1,Y_2,\ldots,Y_m\) i.i.d. \(\sim N(0,1)\) - \(\chi^2\) Distribution:
\(\chi^2\) distribution with degree of freedom \(n\):$ =_{i=1}^n X_i22_n$。 For independent \(\xi_i\sim\chi^2_{n_i},\, i=1,2,\ldots,k\):\(x_{i_0}=\sum_{i=1}^k\xi_i\sim\chi^2_{n_1+\ldots+n_k}\)
\(t\) Distribution:
\(t\) distribution with degree of freedom \(n\):$ T==t_n$
Upper \(\alpha\)-fractile of \(t_\nu\), satisfies \(\mathbb{P}(T\geq c)=\alpha\),$t_{,}={c}(Tc)=,Tt$
\(F\) Distribution:
\(F\) distribution with degree of freedom \(m\) and \(n\):$ F=F_{m,n}$
- If \(Z\sim F_{m,n}\), then \(\dfrac{1}{Z}\sim F_{n,m}\);
- If \(T\sim t_n\), then \(T^2\sim F_{1,n}\);
- \(F_{m,n,1-\alpha}=\dfrac{1}{F_{n,m,\alpha}}\) 。
Some useful lemmas in statistical inference:
For \(X_1,X_2,\ldots,X_n\) independent with \(X_i\sim N(\mu_i,\sigma^2_i)\), then \(\sum_{i=1}^n\left(\frac{X_i-\mu_i}{\sigma_i}\right)^2\sim \chi^2_n\)
For \(X_1,X_2,\ldots,X_n\) i.i.d.\(\sim N(\mu,\sigma^2)\), then $ T=t_{n-1} $
For \(X_1,X_2,\ldots,X_m\) i.i.d.\(\sim N(\mu_1,\sigma^2)\), \(Y_1,Y_2,\ldots,Y_n\) i.i.d.\(\sim N(\mu_2,\sigma^2)\),d enote sample pooled variance \(S_{\omega}^2=\dfrac{(m-1)S^2_1+(n-1)S^2_2}{m+n-2}\), then \(T=\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{S_{\omega}}\cdot \sqrt{\frac{mn}{m+n}}\sim t_{m+n-2}\)
For \(X_1,X_2,\ldots,X_m\) i.i.d.\(\sim N(\mu,\sigma^2)\), \(Y_1,Y_2,\ldots,Y_n\) i.i.d.\(\sim N(\mu_2,\sigma^2)\), then $T=F_{m-1,n-1} $
For \(X_1,X_2,\ldots,X_n\) i.i.d. \(\sim \varepsilon(\lambda)\), then $ 2n{X}=2{i=1}^nX_i ^2{2n} $
Remark:for \(X_i\sim\varepsilon(\lambda)=\Gamma(1,\lambda)\),\(2\lambda\sum_{i=1}^nX_i\sim\Gamma(n,1/2)=\chi^2_{2n}\).
分位数速查
来自 Package stats, version 4.2.1。
其实都可以直接查文档啦(,R 的文档还是很保姆式的。
t-分布模拟
t-distribution 下有四个函数,分别是 density, CDF, quantile function(\(CDF^{-1}\)),还有一个是随机生成一个模拟数组。
dt(x, df, ncp, log = FALSE) 用来计算 PDF 的函数值 \(f(x)\),df 是自由度,ncp 表示非中心化参数
\(\delta\);
pt(x, df, ncp, lower.tail = TRUE, log.p = FALSE)
用来计算 CDF 的函数值 \(F(x)\),注意
lower.tail = TRUE 时计算的是左边值 \(F(x)\),否则实际计算了 \(1-F(x)\)。
qt(p, df, ncp, lower.tail = TRUE, log.p = TRUE)
用来计算分位数,也即 \(F^{-1}(p)\),其他参数意义同上。
一些我的作业里的函数参考:
1 | > qt(1 - 0.025, df = 8) |
这里计算的是 \(t_{8,0.975}\) 的下分位数,实际上是一个 level of significance 为 \(0.05\) 的双尾检验中用到的分位数。
1 | > 2 * pt(-8.529, df = 8) |
这里是在计算一个 P-value,计算的是比 observed data \(-8.529\) 更极端的数据的出现概率,单边是 \(F (-8.529)\),注意此处的“极端”包含比 \(-8.529\) 更小和比 \(8.529\) 更大这两种情况,实际上是 \(F(-8.529) + 1- F(8.529)\)。
由于 t-distribution 是对称的,可以简化为 \(2 \times F(-8.529)\)。
1 | > ncp <- 2.0/0.50 |
这是一个非中心的 t 检验,实际上是在计算 Power Function。
正态分布模拟
常用的三个函数是
dnorm,pnorm,qnorm,含义与
t-分布中的 dt,pt,qt 相似。
1 | dnorm(x, mean = 0, sd = 1, log = FALSE) |
注意一般正态检验中都是使用标准正态分布,也就是不需要去改变
mean 和 sd 的默认值。
1 | > pnorm(0) |
F-分布模拟
1 | df(x, df1, df2, ncp, log = FALSE) |
注意 \(F\)
分布的两个自由度都可以取到无穷,写作 df1 = Inf。
Chi-square 分布模拟
1 | dchisq(x, df, ncp = 0, log = FALSE) |
其他常用 R 命令
持续更新中,基本都是作业里扒出来的。
confidence interval
1 | confint(object, parm, level = 0.95, ...) |
注意 confidence coefficient 的默认值是 \(0.95\),confint
函数是用于拟合模型参数的置信区间估计,例如:
1 | model <- lm(data) |
1 | 2.5 % 97.5 % |
这个附录怎么全咕了啊,不过无所谓了,这课我本来就是在摆烂(
完结撒花
一点都不 happily ever after,说是找到了新的方向,谁知道概率又会不会很艰难呢。
这课明显东西比统计推断多,但是导出成 PDF 一看比统推笔记少了二十多页。
总之都结束了,笑一个吧(


