基础物理光学实验备忘录

考虑到开学之后肯定没空每周研究实验怎么做，最近又很颓不想干活。于是一边补番一边写一份从零开始的，讲人话的实验备忘录，目的是将来做实验前快速阅读一遍，然后对着设计好的实验表和博文就能优雅地动手不动脑地做完实验，还能从这篇备忘录里抄点东西去写实验报告。

这个操作是合理的。我和物理本来就不合适，结合上学期的经验可以发现，无论有没有学过原理，我唯一的解决方案就是按计划一帧一帧地做实验，才不至于大脑空白。加之我秋季学期就没选理论课，理论水平也就是现在这样了，倘若现在不写，将来更写不出来。上学期因为仓促，只在讲义上手写了一些要点，有的时候记不清了就会不知所措，所以这次码个字可以详细一点。

这样的话，物理实验就变成了大猩猩也能做的体力活罢了。我不否认这个想法，也无意论辩这门课是否有意义，将本文视作作者的救命手册即可。

注：未经授权禁止转载，本人不希望在院系里受到关注；所有提到的引用，包括图片，文字，数据信息等，著作权归原作者所有；一概不提供文中提到的自用实验表格，请自行阅读实验讲义，勿直接伸手。

完整报告篇

用单色仪测定介质的吸收曲线

原理简述

一束光入射到有一定厚度的介质上时，有一部分光被反射，另一部分被吸收，其余被透射——也即进入有厚度\(d\)的介质。根据各部分的光强，可以定义出介质板的光谱外透射率\(T=\frac{I_T}{I_0}\)和光谱透射率\(T_{i}=\frac{I_2}{I_1}\)。

（此处应该有图，但是没有图。）

光谱透射率同时与介质的性质和入射光的波长\(\lambda\)​相关。为什么这么说呢？因为忽略介质内散射的情况下\(T_{i}=e^{-\alpha d}\)​，\(\alpha\)​称为介质的线性吸收系数，与介质的性质和入射光波长有关。

经过若干次透射后，透射光的光强为一个等比数列的和，即为\(I_T=\frac{I_0(1-R)^2e^{-\alpha d}}{1-R^2e^{-2\alpha d}}\)​。其中，\(I_{0}\)​为入射光强，\(R\)​为单一界面上的反射率。由此可以计算光谱外透射率\(T=\frac{I_T}{I_0}\)​。

在实际实验中，使用了两块仅厚度不同的试样，计算后近似得出光谱外透射率的比值，我们不加证明地给出吸收系数的近似：\(\alpha=\frac{lnT_{1}-lnT_{2}}{d_{2}-d_{1}}\) 。实际实验中，用微电流放大器的显示值\(V_{1}\),\(V_{2}\)分别替换上式的\(T_{1}\),\(T_{2}\)。

应该做什么？在纸上记什么？

你不懂仪器的构造，但是没关系，跟着做就行了。

校对单色仪的波长示值

单色仪长这个样子：

第一步，通过两个鼓轮调入射狭缝 S1 和出射狭缝 S2 的宽度，分别约为 1mm 和 2mm（目测即可）。

第二步，把汞灯放在 S1 前面，打开汞灯，把手轮转到 577.0~579.1nm 之间的某一位置（通过波长示数器观察）。

显微镜目镜和物镜拧紧放在 S2 前面，调一调高度和与 S2 的距离，观察到像这样的图像。黄的叫谱线，黑的叫狭缝刃口。

关小入射狭缝 S1 使两条谱线分开，在谱线沿缝方向宽度基本均匀、亮度好的前提下， 使狭缝尽量窄，谱线尽量细。再关小出射狭缝 S2，同时微动手轮，使其中一条谱线始终在狭缝中央，直至狭缝宽度与谱线同宽（此时微动手轮，谱线即被遮挡，谱线消失）。

纸上谈兵来说，如上操作可以得到单条谱线的波长示值（显示在波长计数器上）。按这个办法慢慢调波长，在标准值附近分别找两条黄线，一条紫线和一条绿线的示值，把它们记在第一个表里，差值的平均值就是单色仪波长示值的系统误差，之后要修约。

标准值是黄线 579.1nm， 黄线 577.0nm，绿线 546.1nm，紫线 435.8nm。

用汞灯调狭缝宽度

第一步，将单色仪的波长读数装置转到示值在 577.0~579.1nm 之间的某一位置。将出射缝 S2 的宽度暂时调至约 2mm。用显微镜观察汞的两条黄谱线（577.0nm 和 579.1nm）。如果看不到谱线，增加 S2 缝宽或改变波长示值。

第二步，缓慢增加入射狭缝 S1 的宽度，使谱线变宽，直到两条黄谱线刚好碰上且不重叠为止，此时入射狭缝宽约0.8mm。再调节出射狭缝 S2 的宽度，同时微调手轮，使出缝宽度与其中一条谱线宽度大致相同，此时出缝与入缝同宽，约 0.8mm。

此后不要再动单色仪，光强就能满足吸收系数测量的要求。此部分不需要记录数据。

溴钨灯/光路调节，而不是溴钨灯光/路调节

第一步，溴钨灯按讲义上写的接三路输出电源，调整设置。

然后，讲义上是这样写的：

为了减少单色仪的光能损失，提高透光效率（充分利用单色仪的全孔径和相对孔径 D/f），根据图 12 光路图，计算聚光镜和光源的位置。

聚光(透)镜的参数见前面。单色仪焦距 f=300mm (即图 12 的 b=300mm)，单色仪球面镜（准直镜）的光栏宽度 D=50mm。成像规律符合 Gauss 公式。

使球面镜的孔径 D 充分照明，两个相似三角形应有下列关系：d/D=a/b。

翻译成人话：聚光镜摆在狭缝前面 18cm 处，溴钨灯摆在聚光镜前面 9cm 处，注意共轴。当然，得在表格上画个图，装模作样算一下这两个数据。

第二步，手轮调到 610.0nm，调整各种位置。用眼睛靠近出射狭缝 S2 观察红色谱线。

具体怎么调？先粗调后细调。

粗调：溴钨灯电流建议用 2.0A。微调光源的位置，用眼睛观察溴钨灯在入射狭缝 S1 处所成的清晰实像，粗略调节等高同轴。

细调：溴钨灯电流建议用 1.50A。用眼睛靠近出射狭缝 S2 观察光谱，左右(共轴)调节聚光镜至合适位置，不管条纹亮度均匀否，只关注条纹上、下边缘的圆弧左右对称否，调至对称。

再前后、左右微调溴钨灯，眼睛能看到亮度均匀的光谱(条纹)，差不多这样。

调节好透镜和溴钨灯位置后，固定好它们。

最后的仪器安装

第一步，把样品装在 S2 上，先薄再厚，具体操作摘录如下：

将装有钕玻璃吸收片的样品反面的红点对准S2 上红点，顺时针旋转样品，听到咔的声音，样品已锁定，往外拉一下，确认已安装好。

取样品时侧面小螺钉往里轻推，逆时针旋转即可取下。

第二步，装硅光电二极管探头。

将探头插入样品正面的圆柱孔内(插到底)，确认电缆接头处于拧紧状态。

如果还是手笨接不好仪器，就求助一下旁边同学吧，没救了。

测量环节

对每一个样品，观察对各色光的吸收情况。

从 610.0nm 到 550.0nm 转动手轮测定两个最大的吸收峰（光电探测器上的电压示值最小）的波长位置并记录。要求每隔 2nm 测一次示值，在吸收峰左右 4nm 范围内测量点更密，取整数每隔 0.5nm 测量一次，记录在最后一个表里。

注意：测量要消空程，即只向一个方向转动手轮， 一次完成。

测完数据要分析计算什么？画哪些图？

• 根据\(\alpha=\frac{lnV_{1}-lnV_{2}}{d_{2}-d_{1}}\)，列表计算每个波长对应的\(\alpha\)
• 画一个\(\lambda-\alpha\)图，是为吸收曲线。从中读出两个峰值的数值，然后按波长修正规则修一下。
• 误差分析讨论和回答思考题，可参考祖传实验报告。

本文写作中用到的参考

• 单色仪实验操作视频：

  https://www.bilibili.com/video/BV17A411L7mg?spm_id_from=333.337.search-card.all.click&vd_source=6ae5c31a80120436d23cf7b7c7ceb3ba

• 清华大学2021秋基础物理实验(2)讲义

偏振光学系列实验

原理简述

• 什么是偏振光？这不重要

一个单色偏振光可以分解为两个互相垂直的线偏振光的叠加。表示如下：

\[ \begin{cases}{} \ E_x = a_1\cos \omega t \\\\ E_y = a_2\cos (\omega t+\delta) \\ \end{cases} \]

其中的\(\delta\)被称为\(x\)方向偏振分量相对于\(y\)方向偏振分量的位相延迟量。显然，偏振光的“形状”由式中参数决定，主要探讨椭圆、圆和线偏振光的情况。引入偏振方向的概念： \(\alpha=arctan(\frac{a_2}{a_1} cos\delta)\)

我们不加证明地给出关于椭圆偏振光的参数求解式。其中定义\(\psi\)为椭圆的长轴方位角，我也不知道这个是什么意思。

\[ \begin{equation} \begin{cases} \psi &= \frac{1}{2}arctan(tan2\beta cos\delta) \\\\ \frac{b^2}{a^2} &= \frac{2}{1+\sqrt{1-(sin2\beta sin\delta)^2}}-1 \\\\ \beta &=arctan(\frac{a_2}{a_1}) \\ \end{cases} \end{equation} \]

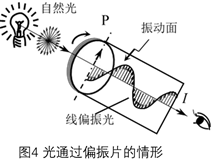
• 偏振片是干什么的？好像是用来产生线偏振光的。

首先，在这张图中，透射轴是偏振片上的那条轴，我们简称为\(x\)轴；消光轴是垂直于偏振片的轴，简称为\(y\)轴。沿\(x\)轴振动光波的光强透射率为\(T_1\)，它接近\(1\)；沿\(y\)轴振动光波的光强透射率为\(T_2\)，它接近\(0\)。二者小比大得到一个很小的值\(e\)，即为消光比。

马吕斯定律：振动方向和\(x\)轴方向成\(\theta\)角的线偏振光，经过偏振片后的透射率为 \[T_\theta=(T_1-T_2)cos^2\theta+T_2\] 提出这个定律有什么意义？

实验中两个偏振片的组合（一个称为起偏器，一个称为检偏器）成为一组仪器。起偏器产生的线偏振光经过检偏器。因此，由马吕斯定律，二者的\(x\)轴夹角即为\(\theta\)。从结论来看，二者的\(x\)轴垂直（\(\cos \theta=0\)）则发生消光现象，二者的\(x\)轴平行（\(\cos \theta=1\)）则透射光强最大。

• 反射和折射时的起偏现象

电矢量形式的菲涅耳公式我看不懂，也不知道是干嘛的（直球）。

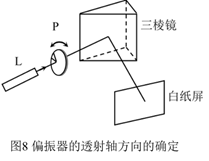
和实验相关的东西翻译成人话来说就是，偏振器的透射轴方向可以由布儒斯特角确定。具体如下：

预置光束在三棱镜上的入射角\(\theta_i\)为\(arctan\text n\)，其中\(\text n\)为玻璃的反射率，也即初入射角约为56°。旋转偏振片到某个角度可以发现白纸屏上的光点很暗。微调二者，使得光点达到最暗时的入射角为布儒斯特角\(\theta_B\)，且此时偏振片的透射轴（\(x\)轴）方向平行于三棱镜上的入射面。

以下与实验无关，可在实验前阅读中跳过。讲义上还有一段关于S分量反射率的叙述，目测是菲涅尔定律的推导：

此时， S 分量的反射率为\(R_{SB}=\frac{(n^2-1)^2}{(n^2+1)^2}\)。

关于反应堆玻片堆：

上式表示的反射率\(R_{SB}\) 一般较小，反射光较弱。光束以\(\theta_B\)射入多块平行玻璃板以获得只有 P 分量的线偏振透射光，经过 N 块玻璃片的 2N 个表面后，S 分量的总透射率为\[(1-R_{SB})^{2N}=[1+(n-1)^2/2n]^{-4N}\]在\(N\)较大时，其值接近于\(0\)。这种起偏装置就叫做玻片堆。

• 延迟器和波片

一般来说，线偏振光入射延迟器后出射为椭圆偏振光。其他的我就一句都没看懂了...不过没关系，一样可以做实验。

实验中需要操作的是判断波片快慢轴，定出方向，做一些测量。我们直接在下一部分说明。

应该做什么？在附的实验表上记什么？

组装仪器

这是一个分光计改装的实验仪。

打开激光器，粗调2,3的轴线，小平台基本水平且与分光计主轴垂直。激光光斑不要太靠近偏振片区域的边缘。

电阻箱阻值100Ω，使得毫伏表示数大于1毫伏。

观测布儒斯特角和偏振器的特性

玻璃片放在平台上，反射面过平台中心点。以下的此为“x”指实验表中的部分填写。

第一步，确定光束正入射棱镜表面时平台方位角\(\alpha_{i=0}\)。用小纸片扎一个小孔，放在激光器出射光束处，调整棱镜表面的反射光在纸屏上的亮点和小孔重合，记下此时的平台方位角即为\(\alpha_{i=0}\)。能不能搞点正常的下标啊

第二步，旋转棱镜使得光束的入射角\(\theta_i\)约为55°。旋转2到某个角度可以发现白纸屏上的光点很暗。微调入射角和起偏器，使得光点达到最暗时的平台方位角为\(\alpha_B\)。起偏器2的方向角为\(P_{\leftrightarrow}\)。能不能搞点正常的下标啊

第二步要连做三次，得到一个平台方位角的平均值\(\alpha_B\)，然后布儒斯特角测量值就是\(\alpha_{i=0}-\alpha_B\)，然后折射率就是布儒斯特角取一个正切值。此为“4”。

第三步，如上得到一个起偏器方向角的平均值\(P_{\leftrightarrow}\)，把2置于平均值位置。拿走玻璃片，转动3使得光强探测器上电压值最小，此时即为正交消光。在表格里记下3上度盘的度数为\(a_\uparrow\)，可以看一下\(a_\uparrow\)是否和\(P_{\leftrightarrow}\)大约相差\(90°\)作为验证，此为“5”。能不能搞点正常的下标啊

第四步，保持偏振器2不动，将3的轮盘角多加\(90\)度，从而恢复到二者\(x\)轴平行的情况。在此基础上每次加上\(0,15,30,45,60,75,80,84,87,90\)度，得到二者\(x\)轴的夹角为以上数据。记下对应的电压值，注意夹角为\(90\)度时可以视作已经消光，示数为环境光光强。此为“6”。

波片的特性研究

第一步，把3的轮盘角调回\(a_\uparrow\)，安装波片\(C_0\)到2盘的度盘上，使得\(C_0\)上白点处对应的直径大致竖直。微调\(C_0\)使得电压示数最小，记录下此时内圈的游标盘示数为\(C_0\)，此时有\(C_0\)的快轴竖直。此为“7”。

第二步，\(C_0\)不动，在小平台上放上\(C_x\)使得光束可以垂直透过。旋转\(C_x\)使得电压示数最小，此时\(C_x\)的某个轴已经垂直于2的透射轴，达到竖直方向。记下此时\(C_x\)的度盘数值，记为\(C_x\)。此为“8”。

第三步，此时二者都不要再动，就有\(C_0\)的快轴和\(C_x\)的某一个轴平行。保证偏振器2的轮盘角为\(P_{\leftrightarrow}\)，偏振器3的轮盘角为\(a_\uparrow\)。然后在此基础上给\(P_{\leftrightarrow}\)加上\(15°\)，转动3的轮盘角使得二者消光（表现为电压示数最小），记下此时的3度盘角度和转动的差值角度。每次测量结束后，将偏振器3的轮盘角归回\(a_\uparrow\)。

还要再做两次，分别给\(P_{\leftrightarrow}\)加上\(30°\)和\(45°\)，调节3的轮盘角。可以发现3的转动差值和给\(P_{\leftrightarrow}\)加上的角度差不多，作为验证。因为这组成了一个半波片。此为“9”。

第四步，转动\(C_0\)，给\(C_0\)加上90°使得\(C_0\)的快轴处于水平位置，和\(C_x\)的某一个轴垂直。与第三步类似地求出3的轮盘角增加差值。可以发现3的转动差值约等于给\(P_{\leftrightarrow}\)加上的角度取负，作为验证。因为这组成了一个全波片。此为“10”。

这几步操作证明了\(C_x\)竖直的“某一个轴”其实是快轴。

单个\(\frac{1}{4}\)波片的特性研究

第一步，取下\(C_x\)，把2归回\(P_{\leftrightarrow}\)，把3归回\(a_\uparrow\)。将2的轮盘角多加\(22.5°\)，于是记录下\(P=P_{\leftrightarrow}+22.5°\)。调节3使得偏振器3的透射轴与偏振器2的透射轴平行，记下此时的轮盘角\(a_i\)。然后转动\(C_0\)，分别记录最大的电压值和最小的电压值。

然后，重复第一步，仅把其中的“\(22.5°\)”分别改为\(45°,67.5°\)实验两次即可。把此过程中的数据都记在表格里，下面的计算暂时先不用管。

第二步，把光源挡住，记一个系统误差电压值\(I_0\)，填在表格边上那个空里面。此为“11”。

测完数据要分析计算什么？画哪些图？

• 计算实验元件玻璃的布儒斯特角和折射率。前文已体现。
• 绘图验证马吕斯定律

用表6的数据分析\(\frac{I_m-I_{min}}{I_{max}-I_{min}}\)和\((\cos x)^2\)之间的线性关系（即二者相等），并绘制一个以\(\theta\)为自变量的图，体现\(\frac{I_m-I_{min}}{I_{max}-I_{min}}\)和\((\cos x)^2\)两条曲线的变化。其中\(I_{min}\)和\(I_{max}\)分别代表\(\theta\)为\(90°\)和\(0°\)时的光强测量值。

• 观测偏振光通过半波片和全波片的现象。前文已体现。
• 线偏振光通过\(\frac{1}{4}\)波片

其实就是把表格补满的过程。

其中，计算波片相延可以使用\(|sin\delta_r|=\frac{2\sqrt{(I_{min}/I_{max})}}{sin(2\beta)(1+I_{min}/I_{max})}\)来计算。三个值都略小于\(90°\)。理论值均为\(90°\)。

用\(\alpha\)计算长轴方位角则有\(\psi\)和\(\alpha\)相差\(90°\)，但要把\(\psi\)调到\([-90°,90°]\)的范围内。三个理论值分别为\(0°,45°,90°\)。

用公式计算长轴方位角，则把\(\psi=\frac{1}{2}arctan(tan2\beta cos\delta)\)代入算一下即可。理论值罗列同上，应该差距不大。

其余分析参考祖传实验报告即可。

本文写作中用到的参考

• 清华大学2021秋基础物理实验(2)讲义

• 清华大学2011级尚恩垚学长的大物实验报告《偏振光学实验》

（说来惭愧，我一个学基物的，看了别人的大物实验祖传报告，才学会了这个实验x）

塞曼效应实验

待填坑。

光栅衍射实验

笔者直到实验结束也没明白这是在做什么。

放一个我自己的实验报告在这里，希望将来的社恐同学们不要再被困扰到了，到期末我会把信息脱敏后上传 GitHub 和课程资源共享计划。Click Here

简要报告篇

摩擦系数实验

为什么这学期会有这么个实验...

是新出的题目，暑假期间没有拿到讲义，可能不会写了。

弗兰克-赫兹实验

原理简述

完全看不懂，拉倒吧。总感觉也不影响实验

应该做什么？

第一次实验的接线

实验仪“放大倍数”档位选择“\(×1\)”档，“扫描选择”档位置于“手动”档。打开一体机电脑。参考讲义上的\(10(a)\)给实验管箱接线（或者照抄上图），检查无误后准备通电。

通电时先打开实验仪背后红色按钮，再按下实验仪前面的“灯丝电流开关”（若不按下此按钮，灯丝电流输出为 0A）。然后在实验仪上调整灯丝电流在\(0.8A\)附近，拒斥场电压在\(7.5V\)附近，控制栅电压在\(1.5V\)左右。

寻找实验条件

缓慢在实验仪上增加扫描电压\(U_a\)，观察板极电流\(I_p\)的变化情况。 当看到其起伏变化时，分别改变实验仪上的三个参数，定性观察每个参量对\(I_p\)的影响。如果随着\(U_a\)的增加在 \(0 ∼ 85V\) 内能大致观察到\(I_p\)有 \(6\) 个峰，峰与谷的差别相对比较明显，则达到最佳测试条件。此时把实验仪上的档位切成自动扫描，启动自动采集软件绘制曲线，获取峰值电压。

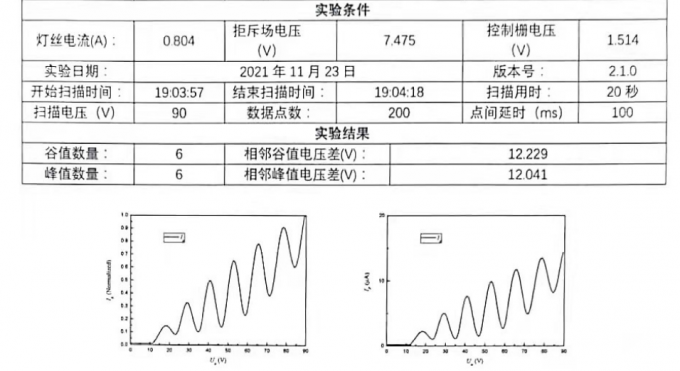
太抽象了，所以我找了一份实验数据，来自刘丁菡学长，大概这样：

注意以下要点：

• 实验仪上的灯丝电流不能一次改变很大，大概在\(0.01∼0.02A\)左右；调整灯丝电流后要等两三分钟再观察\(I_p\)的变化，有一个滞后。
• 扫描电压\(U_a\)较大时尽量使用自动挡位测量，用完之后尽快调零。如果出现电流表指针打表，要尽快调小扫描电压，关闭灯丝电流的开关。

跟着FH软件教程操作

按照教程一直做到第三步，第四步校准仪器的时候输入自动扫描电压\(U_a\)的最大值为\(90V\)，扫描出完整的\(6\)个峰和谷。第五步数据采集模块中选择数据个数为\(200\)，点间延时为\(100ms\)为最佳。此后一直根据教程行动即可，得到第一份数据。

定性研究的操作

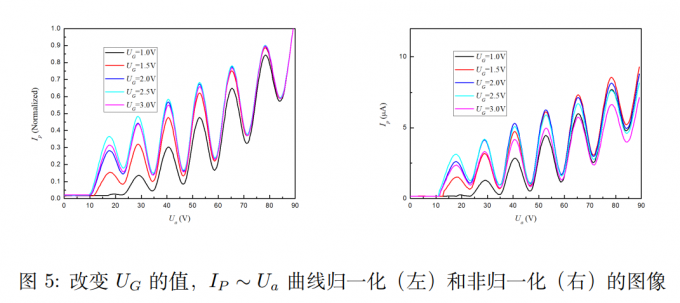
保持灯丝电流和拒斥电压不动，改变控制栅电压在\(1.0V,1.5V,2.0V,2.5V,3.0V\)这些值上变化，扫出曲线。

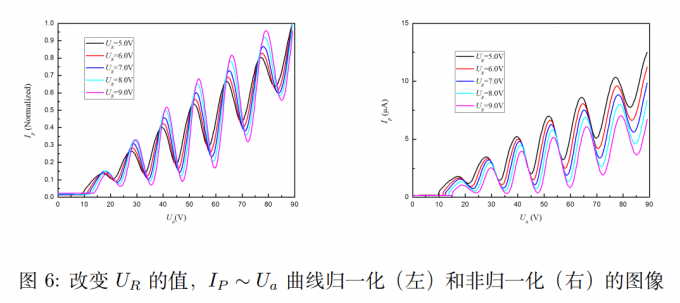
保持灯丝电流和控制栅电压不动，改变拒斥电压在\(5.0V,6.0V,7.0V,8.0V,9.0V\)这些值上变化，扫出曲线。

氩原子更高激发态的情况

这一次是两人一组，等待大佬救我

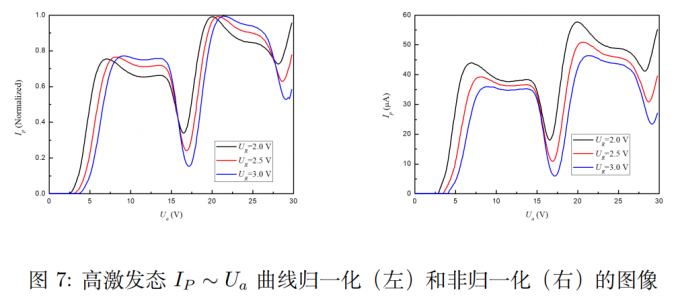
类似的操作，把亚克力板接进电路，设定最佳实验条件。在软件上调整扫描电压最大值为\(30V\)​。在实验仪上调整灯丝电流在\(0.78A\)附近，控制栅电压在\(1.5V\)左右。拒斥场电压分别调整为\(2.0V,2.5V,3.0V\)。类似扫描出\(I_p-U_a\)的归一化和非归一化曲线。

注意以下的要点：

• 只需要图上有两个峰。第二个峰大约出现在\(25V\)左右，因此最大扫描电压只需要\(30V\)。而且\(I_p\)的最大峰值对应不超过\(50\mu A\)。
• 祖传报告中指出这一步实验仪上的另两个参数保持不变即可，和讲义不是很一样。我倾向于相信祖传报告。

实验结束后可以断开其他元件的连接，整理仪器，处理自己的数据。

测完数据要分析计算什么？

测试\(I_p-U_a\)曲线，得到氩原子第一激发电位

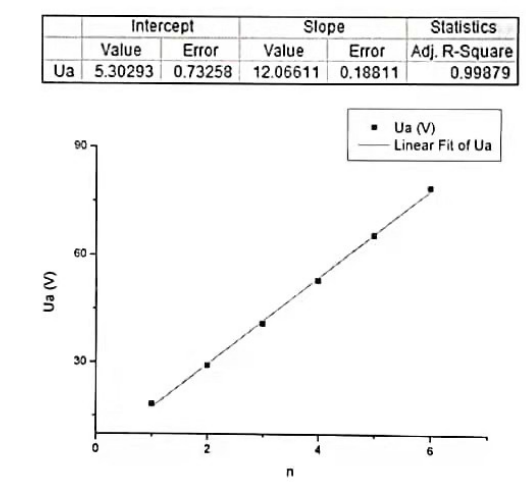
找到第一部分数据的 Excel 表格 Data 页，取六个峰值的电压数据和测量次数（注意舍去一看就不对的值），到 Origin 里拟合数据。由于曲线上相邻两峰值之间的电位差就是氩原子的第一激发电\(U_g\)，因此处理得到的斜率就是第一激发电位。

太抽象了，这是一张示例处理表格，来自刘丁菡学长，其中的 \(Slope-Value\) 就是所需要的值。

关于不确定度的计算，公式都在下面了：

\[\Delta_A=S_b=b\sqrt{\frac{2(1-R^2)}{n-2}}\]

\[\Delta_B=0.001×b+0.01\]

\[U_g=(b±\Delta_{U_g})\]

其中\(b\)是斜率，\(R^2\)是拟合的最后一列方差，\(n\)是实验次数（即为\(6\)），\(\Delta_{U_g}\)是两个系差平方和的开方。

氩原子受击后回到基态辐射出的光波波长

套下面两个公式：

\[\lambda=\frac{hc}{eU_g}\]

\[\Delta_\lambda=\lambda\frac{\Delta_{U_g}}{U_g}\]

实验中观测不到发光是因为这是紫外波段而不是可见光波段，也因此用壳罩住了管子防止对人体造成伤害。

定性研究栅极电压和拒斥电压对\(I_p\)的影响

控制栅电压的影响：由图可知，从峰值对应的扫描电压上看，随着 \(U_G\) 值的增大，曲线中峰 值所对应的扫描电压值稍向左偏移；从峰值的相对大小来看，随着 \(U_G\) 值的增大，峰值先增大后减小，在 \(U_G≈ 2.0V\) 附近能观测到峰值最大，说明此时单位时间到达极板的电子最多。 理论解释见祖传报告，反正我也写不出来。例图如下，来自刘丁菡学长：

拒斥电压的影响：由图可知，随着 \(U_R\) 值的增大，曲线绝对值下移、峰谷值之间的差距变 大、曲线中峰值所对应的扫描电压值稍向右偏移。理论解释见祖传报告，反正我也写不出来。例图如下，来自刘丁菡学长：

更高激发态的研究

例图如下，来自刘丁菡学长。\(U_R\) 整体对曲线的影响与第一激发态是类似的，即随着 \(U_R\) 的增大，曲线整体下移，峰谷差值增大，峰值向右移动。但差别在于曲线的形状有所不同，即没有出现很明显的一个峰值，而是峰值附近有一个小平台。理论解释见祖传报告，反正我也写不出来。

解答思考题

见祖传报告。

本文写作中用到的参考

• 清华大学2020级刘丁菡学长的基物实验报告《弗兰克-赫兹实验》

感谢学长的图救我老命，不然这个实验真的看不懂在干嘛...

几何光学系列实验

不喜欢系列实验，真的好麻烦。

原理简述

会算相似三角形就行

• 薄透镜的成像规律

经典公式：\(\frac{1}{f}=\frac{1}{p}+\frac{1}{q}\)，其中 \(p\),\(q\) 分别代表物距和像距；\(\beta=-\frac{q}{p}\)称为线放大率。

它们有很多正负性质的要求：前三者实物/实像/凸透镜为正，虚物/虚像/凹透镜为负，\(\beta\)在实像时为负，虚像时为正。

• 内调焦望远镜

望远镜是由一个物镜一个目镜组成的。当我们用一组物镜组替代物镜时，不必移动物镜和目镜间的距离\(l\)，而是直接改变物镜组的焦距即可达到整体调焦的效果。这就叫做内调焦望远镜。

实验中用到的物镜组是一个凸透镜\(L_1\)和一个凹透镜\(L_2\)组成的。这是一个最简单的变焦物竞组物镜组。原理是\(L_2\)的物方焦点在\(L_1\)的像方焦点右侧时，改变两个透镜的间距\(d\)就能达到内部调焦的效果。此时取二者的“正焦距”（我不太会描述）为\(f_1'\)和\(f_2\)，物镜的组合焦距即为\(f_o'=\frac{f_1'f_2}{d+f_2-f_1'}\)。要求满足\(f_1'-f_2<d<f_1'\)才能如上调节。

我们把目镜的焦距记作\(f_e\)。望远镜的视放大率即为\(\Gamma_T=-\frac{f_o}{f_e}\)。这个数值的绝对值越大，观察到的像越大。比如说，观察远物的时候可以通过调小\(d\)来放大\(f_o\)，观察近物的时候不想改变物镜组和目镜组之间的距离，直接放大\(d\)即可。

应该做什么？

A0.薄透镜成像规律

为了满足近轴光线条件，要进行共轴调节。

粗调的时候，先把光源，物，透镜靠拢，调节到中心大约在一条平行于导轨的直线上。总之怎么看着舒服就怎么调。

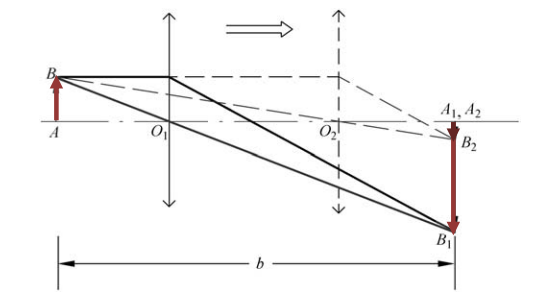
细调的原理是大象追小象大像追小像。当物与像的距离大于 \(4f\) 时，凸透镜从物移到像的过程中会成两次清晰的像，一大一小。要做的就是移动像和透镜的位置，使得\(B_1\)追上\(B_2\)，也即两个像差不多大，这可以通过像屏上的坐标贴纸判断。此时像在透镜的主光轴上。

不要动平行光管，就是那个挺长的不认识的东西。此处无记录要求。

B1.物像距法测量薄凸透镜焦距

这很明示了，读个数据套公式就行。

B2.共轭法测量薄凸透镜焦距

读个数据套另一个公式：\(f=\frac{b^2-a^2}{4b}\)，其中 \(a\) 指两次透镜位置间距离。

B3.焦距仪法测薄凸透镜焦距

读六组数据写在表格上，比较麻烦的是算不确定度。这一部分已经在讲义和实验表上详细手写了，照做即可，不再打一遍了。

C1.主面间距测量

5中的C.2应为B.3。不过我不太懂怎么通过这几个参数算主面间距，好怪。此处留坑。

C2.修正共轭法系差

again，算就对了。

D.用焦距仪测凸透镜的焦距的附加透镜法

这个讲义上也说的挺清楚的。注意先给玻罗板取某一线对记录下来，第一步和第二步要用一样的线对（废话）。

最后的凹透镜焦距是\(f_2=-\frac{f_1 y_0}{y''}\)，由于是凹透镜的原因，焦距记为负的。

E.内调焦望远镜的物镜组研究

第一步，分别对物镜组中的凹凸透镜进行共轴调节，用焦距仪法测此组光具焦距值\(f_o'\)作为物镜焦距。反推得到此时凹凸透镜的距离\(d=\frac{f_2f_1'}{f_o'}+f_1'-f_2\)。其中，由于凹凸透镜的焦距已经在B和D实验中测出，直接取用其值即可。

第二步，改变凹凸透镜距离使得长焦透镜\(L_1\)距离测微目镜约\(10cm\)。得到第二个测量值。

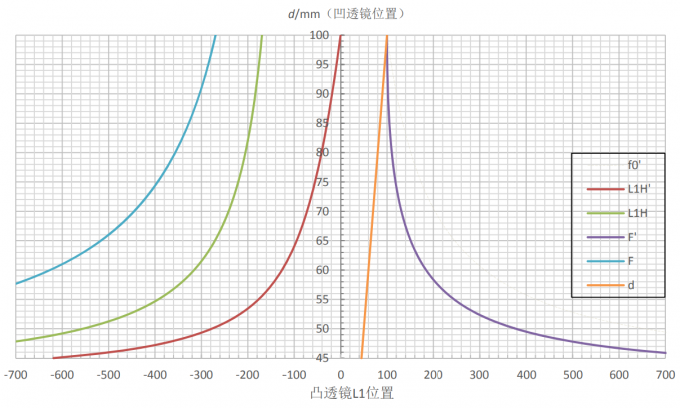
第三步，分别假设凹凸透镜的焦距，然后画一个类似下图的图。

这张图的逻辑是：以纵轴表示自变量\(d\)，横轴表示四个因变量。其计算公式分别为：

\[l_{L_1H}=-\frac{f_1'd}{d+f_2-f_1'}\]

\[l_{L_1H'}=-\frac{d(d-f_1')}{d+f_2-f_1'}\]

\[F'=l_{L_1H'}+f_o'\]

\[F=l_{L_1H}-f_o'\]

其中，凸透镜\(f_1'=0.3m\),凹透镜\(f_2=0.2m\)。所以这个图是不是实验之前就能画出来

本文写作中用到的参考

• 透镜焦距实验-仪器详解

https://www.bilibili.com/video/BV163411q7NP?spm_id_from=333.999.0.0&vd_source=6ae5c31a80120436d23cf7b7c7ceb3ba

• 清华大学2011级耿强学长的大物实验报告《透镜焦距的测定》P181

写在最后

我一向把物理实验当成“可以摆弄仪器的好玩的课”，高中学竞赛的时候就羡慕物化生竞赛的同学可以做实验，我们只能一直待在教室里写题。但是哪怕基物实验 1 拿了 A-，对于实验的原理仍然不甚了解。到最后每学期六次做实验三次写报告成为了生活中的调剂，不用太动脑子就能写出一大片东西，好像自己很努力一样。

在 Overleaf 上无意间找到了清华大学近代物理实验报告模板。朱老师的要求和这个还是很不一样。发现也没有用于普通实验的模板，于是改了改我的自用模板，还行。

GitHub 地址：https://github.com/Chiyuru/THU-Fundamental-Physics-Report

但是用 LaTeX 写实验报告的人哪个没有自己的模板啊

您又在假装干活了是吗